人工智能学习笔记-update_Nov. 2024

内容目录

机器学习基本概念

机器学习是人工智能领域非常重要的技术，这个名词本身是一个宽泛的概念，泛指一类可以从既有经验中进行学习的强大技术。深度学习是机器学习中的一个分支，而神经网络是机器学习中的一类算法。随着神经网络的不断发展，如今，深度学习往往与神经网络（或深度神经网络）划等号。

所谓学习，指的是一个训练模型的过程。一个可以达成某种目的、有一系列经过可调参数的程序便是所谓的模型。训练模型所基于的材料则是大量的数据。由此，我们可以说，机器学习的本质，就是从原始数据中提取模式的能力。这个过程少不了以下基本要素：

用于学习的数据 (data)
用于转换数据的模型 (model)
用于量化模型有效性的目标函数 (objective function)
用以调整参数、优化目标的算法 (algorighm)

数据集由一个个数据样本(sample)组成，大多数时候，一个数据集中的样本拥有数量相同的特征类别，即它们的特征向量是固定长度的，这个长度被称为数据的维数(dimensionality)。这样的数据显然更易于高效处理，为批量计算带来很大方便。

根据学习数据的不同，机器学习大致可以分为监督式和无监督式两类算法。

决策树

决策树，属性，重要性度量

监督学习(supervised learning)

期望实现一个通过给定输入特征进行预测的模型，通过对数据的学习，寻找特征与标签之间的映射关系。一个著名的标注了样本标签的数据集是Iris鸢尾花数据集，每个单独的植物对应一个样本，每个样本标注了四个特征标签：花瓣长度、花瓣宽度、花萼长度、花萼宽度。
典型的监督学习任务：分类(classification) - 图片分类、回归(regression)- 市场价预测

无监督学习(unsupervised learning)

用于训练含有很多特征的数据集，但样本没有标签。模型需要学习出其中的概率分布或者有用的结构性质。
典型的无监督学习任务：

聚类(clustering) - 将数据集中的样本分成不同的组（被称为一个簇 cluster）。目标是使同一簇内的样本具有较高相似性，不同簇之间的样本具有较大的差异性。簇指的就是一组相似数据点的集合，在某种度量下彼此更接近，而与其他簇中的数据点更远。聚类算法试图在数据中发现这些隐藏的簇，以便对数据进行分组、分类或者降维等操作。

高维数据可视化（High-Dimension Visualization）- 通过降低维度，将数据点在二维或三维空间中可视化，从而发现数据之间的关系、模式或者异常。常见的高维数据可视化方法包括主成分分析（PCA）、t-SNE等。

生成模型（Generative Models）- 捕捉输入数据概率分布的模型。一旦模型学习了数据的概率分布，它就能够生成更多的数据点（与训练数据类似的新样本）。这对于增强分类器的鲁棒性非常有用。生成模型可以是概率图模型、自动编码器、变分自编码器等，还可以用于生成图像、文本、音频等。典型的生成模型有生成式对抗网络GAN。

机器学习往往涉及数据转换，简单的模型可以处理一些单一的问题，例如对比一组传入数值（如传感器检测脉搏）和标准数值（健康脉搏的区间）的异同。但随着需求难度的提升，传统的经典方法无法解决更复杂的问题。如今广受关注的深度学习(deep learning)，则是一种特定类型的机器学习，具有强大的能力和灵活性。深度学习使用错综复杂的神经网络，其中包含很多层的数据转换。

2. 回归问题与平方损失函数

机器学习处理的最简单的一类任务是一元线性回归，在给出的数据集中需要寻找到一条最佳拟合数据趋势的直线。

$$ y=wx+b \qquad \qquad (式1.1)$$

在这一模型中只有一个自变量x，w代表权重(weight)，b代表偏置(bias)。学习的目标就是根据样本数据确定参数w和b的值。

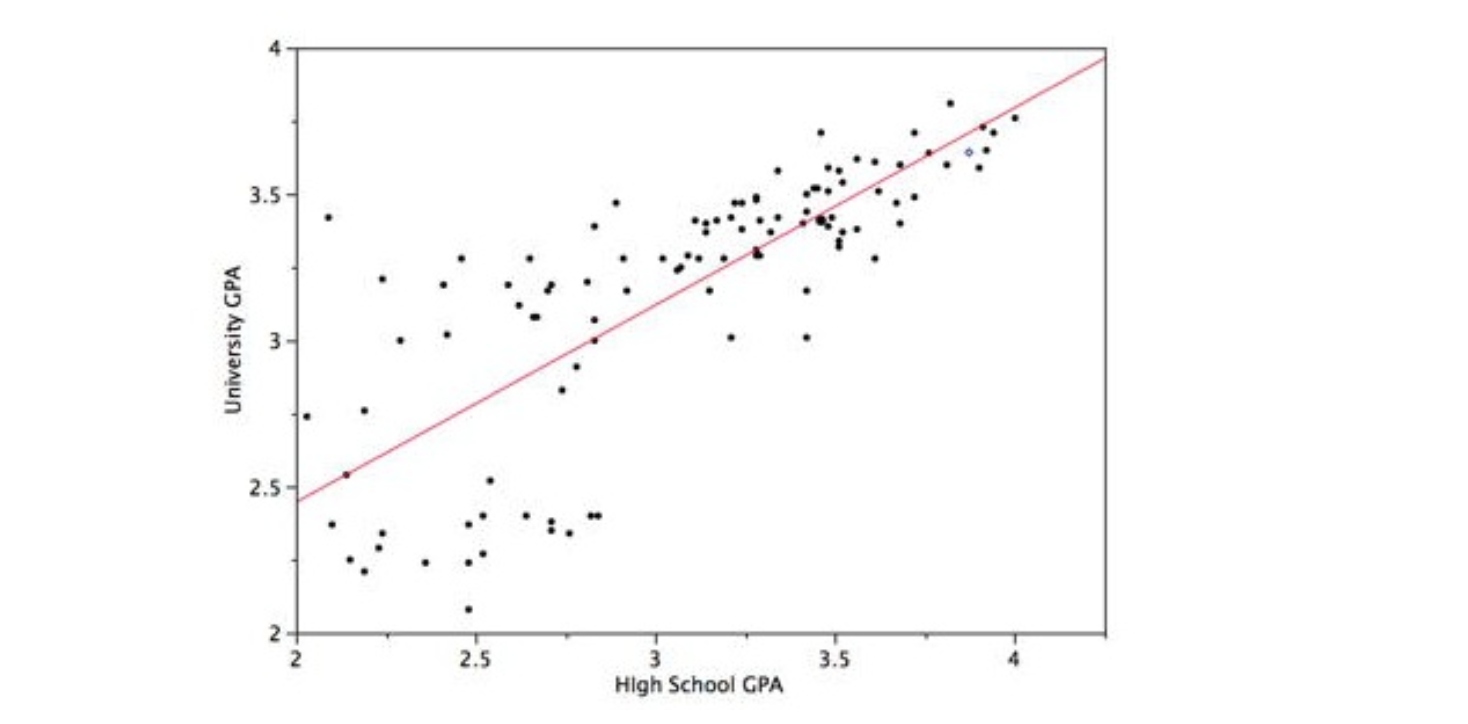
一个线性模型的优劣，可以通过考察模型预测值与实际值之间差异程度来衡量。这个差异一般称为“残差”或者“拟合误差”，可以表示为 $ y_i - \hat{y_i} $，其中 $\hat{y_i}=wx_i+b$ 是模型输出的预估值。一个好的拟合模型，显然要求残差达到最小。对于一个数据集中的所有训练样本，就意味着全部残差的总和要达到最小。这一总和可以表示为一个求和函数 $ \sum(y_i - \hat{y_i})$ 。考查残差以衡量模型的优劣是机器学习算法中的基本要素，计算差值的函数称为损失函数。

【笔记补充】机器学习所说的“学习”，本质上就是根据训练数据更新参数的过程，学习有“进步”就意味着新的参数设定使得模型输出结果越来越接近标签值。换言之，模型的更新迭代过程，就是通过衡量模型输出的优劣、进而调整参数使其与目标值的差异越来越小的过程。用于衡量模型的就是损失函数，它返回一个数值，告诉我们预估值与目标值的差异程度。

式1.1有明显的数学缺陷，因为预估值可能有的高于目标值，有的低于目标值，残差就会有正有负，将这些数字加和显然会出现正负抵消的情况。考虑到残差计算的合理性以及后续通过求导来计算损失函数最小值等因素，一元线性回归问题实际使用的损失函数这样计算：
$$ Loss = \frac{1}{2}\sum\limits _{i=1}^n (y_i - \hat{yi})^2 = \frac{1}{2}\sum\limits {i=1}^n (y_i - (wx_i+b))^2 \qquad (式1.2)$$

这一函数被称为平方损失函数 (Square Loss)。这一函数不仅计算方便、保证了残差非负，而且刚好表达出了每个数据样本点与其估计值之间的欧式距离大小，具有很好的几何意义。对于n个数据，将这一误差总和除以n便得到了均方误差：
$$ Loss = \frac{1}{2n}\sum\limits _{i=1}^n (y_i - \hat{y_i})^2 \qquad \qquad (式1.3) $$
这是目前使用最广泛的损失函数之一。

损失函数的目的是求得使损失函数值达到最小的w和b（模型参数），于是，寻找最佳拟合模型的任务就转变为了一个求函数最小值的数学问题。函数极值点上的导数为零，因此对于这个函数，我们需要对w和b求偏导：
$$ \frac{\partial Loss}{\partial w}=(y_i-b-wx_i)(-x_i)=x_i(wx_i+b-y_i) \
\quad \
\frac{\partial Loss}{\partial b}=(y_i-b-wx_i)(-1)=(wx_i+b-y_i) \
\quad \
\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (式1.4)$$

不断调整参数使得偏导为零就是模型学习的最终目标。

3. 回归问题损失函数与梯度下降

现实世界中，我们面临的样本几乎都有多个属性，要处理的往往是由多个属性值构成的特征向量。因此，回归模型将不再是仅有一个自变量的函数。假设样本有m个属性，不同属性对应不同权值，模型可以表示为：
$$ \hat{y} = w_1x^1 + w_2x^2 + ... +w_mx^m + b \qquad (式1.5) $$

（为了与样本序号 $x_i$ 区分开，属性用上标来表示）
更为简洁的表达方式是使用向量。另外，式1.5中的偏置b可以理解为 $w_0$，并且设 $x^0=1$ ，这个模型就可以简化为向量相乘的形式：
$$ \hat{y} = W X \qquad \qquad (式1.6) $$

对于实际运算来说，这里的表达式应该是 $\hat{y}=W^TX$ ，即将原本的行向量转置成列向量以方便进行矩阵运算。本文理论部分只表达公式，不进行计算，因此尽量简化标注。

代入平方损失函数后得到：
$$ Loss = \sum\limits _{i=1}^n (y_i - W X)^2 \qquad (式1.7) $$
由于数据集中有n个样本，X和Y都可看作一个n维向量。而每一个样本 $x_i$ 都是一个m+1维的向量（从$m_0$ 开始），因此X其实是一个n行m+1列的矩阵。同样，要通过求损失函数的极小值来寻找最佳的参数W。

线性回归模型最终演变为损失函数求极值的问题。对于简单的函数尚且可以通过公式推导求得解析解，但大多数情况下，它并不能作为一个通用方法，而是需要采用近似计算的方式寻求数值解。
假设一个二维平面中的凸函数，我们可以通过迭代法一步步下降x的取值求得函数最小值，这个下降过程的步长的选择将影响计算的效率。在曲线较陡的地方，步长最好大一些，从而加快下降的速度，反之曲线平缓的地方，步长最好小一些，以避免错过极值点。因此，可以利用斜率来调整步长。

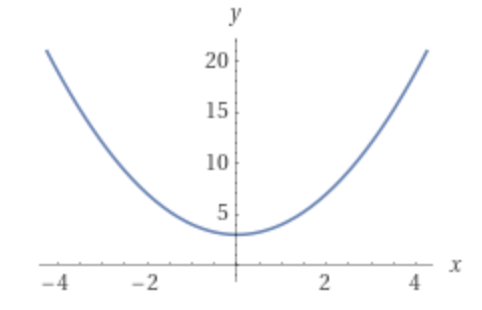
由此，可以将步长表示为 $\eta \Large \frac{\delta y}{\delta x} $，其中， $\eta$ 是一个常数，在机器学习中表示学习率（也可以称为步幅step size），它通常是一个很小的值，比如0.1或者0.001。
x的迭代更新过程可以表示为：
$$ x^{(k+1)} = x^{(k)}-\eta \frac{\delta y}{\delta x} \qquad \qquad (式1.8) $$
第k次迭代的x取值减去步长，就是下一次（第k+1次）迭代的x取值，即每一次的取值都是在上一次基础上减去一小段步长。利用斜率的变化，步长实现了自动调整（斜率大时步长大，斜率小时步长也小），从而更合理的更新x的迭代取值。

在二元函数中同理，假设一个二元函数 $z=f(w,b)$ ，在w方向上的迭代和b方向上的迭代就可以用它们的偏导分别表示为:
$$ w^{(k+1)} = w^{(k)}-\eta \frac{\partial f(w,b)}{\delta w} \
\qquad \
b^{(k+1)} = b^{(k)}-\eta \frac{\partial f(w,b)}{\delta b} \
\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (式1.9) $$
在w方向上的偏导和在b方向上的偏导共同构成的向量便是梯度 $(\large \frac{\partial f(w,b)}{\delta w},\frac{\partial f(w,b)}{\delta b})$。空间中的某一点，在所有可能的变化方向中，变化最快（即变化率——方向导数最大）的就是梯度，更正式的梯度表达式如下：
$$ \overrightarrow{grad} f(w,b) = \frac{\partial f}{\delta w} \vec{i} +\frac{\partial f}{\delta b} \vec{j} \qquad (式1.10) $$

更常见的简单符号是一个倒三角：
$$ \nabla = \left[\begin{array}{c} \frac{\partial f(w,b)}{\delta w} \
\qquad \
\frac{\partial f(w,b)}{\delta b} \end{array} \right] \qquad (式1.11)$$

迭代过程中，每一步都沿着变化率最大的梯度方向移动，就能以最快的速度抵达极值点，这样的方法就是梯度下降法。

4. 分类问题的分类器函数与损失函数

机器学习大致分为回归与分类两种任务，分类问题也称逻辑回归(logistic regression)，这个说法与回归任务的术语——线性回归(linear regression)很容易令人混淆。本文使用最简单清晰的说法：回归、分类。

常见的分类问题：垃圾邮件识别、图片分类等。分类器对输入的数据进行自动识别，输出离散值（某个类别）。MNIST手写数字识别训练中，输入的每个样本是28x28=784维的特征向量，模型需要输出0～9共十种类别/离散值

4-1 二分类，sigmoid，交叉熵

分类问题中最简单的一种就是二分类，可以猜想到这种分类器的输出往往就是1/0。建立一个简单的二分类模型只需要在线性模型的基础上增加一步运算，将原输出值按照我们的分类标准划分为两个互斥的区间即可（比如设定一个阈值，大于它就输出1，小于它就输出0）。符合这一特性的正是阶跃函数。
$$ \text{单位阶跃函数} \qquad y=
\begin{cases}
0 & a<0 \ 1 & a\le 0 \end{cases} \qquad \qquad (式1.12) $$

（注：为了与后文神经网络部分中，来自《深度学习入门》书中的内容相对应，暂且采用a作为激活函数和分类函数的自变量，它表示输入信号x经过线性计算后得到的结果 $a=wx+b$ 。但在更多的深度学习类书籍中，将会看到z作为自变量。下一章的激活函数板块中的公式开始将恢复使用z)

阶跃函数的缺陷是十分明显的，现实世界中的数据分布广泛而随机，对于一个靠近临界值的数据，它应该归属为哪一类是有争议的。我们更需要一个连续、光滑的函数作为分类器。对数几率函数（sigmoid函数）就是符合这一要求的选择，从图像上看，可以把它视作阶跃函数的改进版（尽管它们是截然不同的函数）。

$$ \text{sigmoid函数}\qquad \sigma (a) \equiv \frac{1}{1+e^{-a}} \qquad \qquad (式1.13)$$
(注：本文用 $\equiv$ 表示"defined as")

【笔记补充】 sigmoid 函数 $\large \frac{1}{1+e^{-a}}$ 也称对数几率函数，在机器学习典型任务——逻辑回归中用作分类器，它不仅能够输出样本的预估类别，还能给出属于这一类别的概率。
当需要对线性回归模型输出的预估结果进行分类时，只需在原模型基础上增加一个阶跃函数即可使其转变为分类器。但阶跃函数的分类是十分“硬性”的，无法表达处于中间模糊地带的数据情况。对数几率函数可以实现分类的同时又是连续光滑的，且具有单调性、任意阶可导等优点，因此是合格的分类器。
“对数几率”的含义：将 $y=\large \frac{1}{1+e^{-a}}$ 重新整理可以写成对数形式：$a=\ln \large \frac{y}{1-y} $ ，y可以理解为事情“发生”的概率，1-y就是“不发生”的概率。所以它们的比值就是事情“发生”对“不发生”的几率（相对可能性），对几率求对数因此就称为“对数几率”函数了。

sigmoid函数的重要意义：将输出数值限制在0～1之间，表示输入值被映射到概率的范围。

在线性回归问题中，一般使用平方损失函数或均方误差函数(式1.3、1.7)。而在分类问题中，一般用交叉熵 (cross-entropy) 作为损失函数。交叉熵公式在不同的情况下会有不同写法，针对二分类模型可以直观的表达为：

$$ Loss = -\sum\limits_{i=1}^n [y_i \ln \hat{y} + (1-y_i)\ln{(1-\hat{y})}] \qquad (式1.14) $$

这一式子中，$y_i$ 是标签（0或1），$\hat{y}$ 是模型输出（取值在0～1之间，无限接近0或1）。这个式子虽然看起来是个比较繁琐的多项式，但在实际计算时，真正参与计算的只有加号两边的其中一项。比如当标签为0时，实际参与计算的就只有 $\ln{(1-\hat{y})}$，当标签为1时，实际参与计算的只有 $\ln \hat{y}$ 。

【笔记补充】交叉熵的含义：The term "cross entropy" comes from information theory, where it is used to measure the difference between two probability distributions. Specifically, it is a way to quantify the amount of information needed to encode events from one probability distribution using the optimal code for another distribution.
In the context of machine learning, particularly in the realm of classification problems, cross entropy is commonly used as a loss function. The name "cross entropy" emphasizes the comparison or interaction between two probability distributions: one that represents the true distribution of the data (the target or ground truth), and another that represents the predicted distribution produced by the model.
The term "cross" in "cross entropy" signifies the interaction between these two distributions, as the loss function measures the average number of bits needed to encode events from the true distribution when using the optimal code for the predicted distribution. It's a measure of how well the predicted probabilities align with the actual probabilities.

交叉熵损失函数的重要意义 ：当我们试图了解一个模型的准确度时，可以简单地用预估正确的个数除以总测试样本个数得到一个“准确率”，但其中的细节会被忽略掉，比如预估值与标签值的离得有多近（准确的程度）等。交叉熵函数能够反映出概率间的误差，即使两次结果有同样的准确率，但其中的概率分布可能有很大不同。

4-2 多分类, softmax，交叉熵

在二分类问题中，分类器的sigmoid函数输出一个具体数值，但在多分类问题中，模型的输出需要采用向量的形式，样本对应的标签也同样以向量来记载，并且会用到被称为"one-hot"独热编码的形式，即在正确的分类位置上数值1，其他位置均为0。比如在Iris鸢尾花训练集中共有三个花种，需要输出三个类别，它的训练模型输出就是一个有三个元素的向量，所对应的标签也一样。在MNIST手写数字识别中，需要识别0～9共十种数字，即十个类别，因此它的输出和标签都是10个元素的向量。

与sigmoid的概率想法一致，多分类问题也同样需要输出各个预估值的概率，无论有多少种类别需要预测，所有输出值（概率）的总和应该为1。符合多分类需求的分类器是这样一种函数：
$$ \text{softmax 函数：} \qquad y_k=\frac{e^{ak}}{\sum\limits{i=1}^n e^{a_i}} \qquad (式1.15)$$
$y_k$ 表示第k个输出节点。这一函数首先将a进行指数运算，这将拉开数据间的差异（经过指数运算，大数变得更大，小数变得更小），之后用这个结果比上所有这些“指数化”了的a的总和，这一比值就是它在总和中的占比，这便得到了0～1之间的概率值，且所有输出总和为1。

【笔记补充】 "soft"的含义：输出层的计算是在寻找最终答案，这个答案就是所有输出中的max最大值，或者说最大可能性。定位最大值非常容易，python中可以轻易获得一个列表的最大元素及其索引，这是一种很硬性的、极端的“hard”方式——最大值输出的可能性是百分之百，其他不是最大值的元素出现的可能性是零。但softmax函数给出了一种不那么“硬性的”选择，它返回的结果是每一项输出“成为最终结果的概率是多少”，而非简单的选择最大值、摒弃所有其他值。
Softmax函数是对数几率函数在多分类问题上的推广，对数几率函数可以看作softmax函数的一种特例。

同样的，面对多分类问题，我们的损失函数也要随之扩展。在多分类问题中，交叉熵函数需要更新为：

$$ Loss = -\sum\limits{i=1}^n \sum\limits{k=1}^C y{ik} \ln \hat{y}{ik} \qquad (式1.16) $$

i是样本索引，总计n个样本。k代表分类中的第k类，总计C个类别。
$y{ik}$ ：第i个样本属于第k类的标签
$\hat{y}{ik}$ : 第i个样本属于第k类的预估(模型输出)

注：Iris鸢尾花分类和MNIST手写数字识别都是典型的互斥型分类问题，本文尚未涉及非互斥型分类问题。

以上是机器学习所涉及到的最基本的算法原理，神经网络结构中，各神经层的计算就建立在这些算法上。因此在下文中，会再次看到本章中的很多函数。

神经网络基础

1. 基本概念

感知机的出现

神经网络的最初想法早在近一个世纪以前就已出现，但真正的发展却是从2006才开始。深度神经网络(deep neural network)技术的发现带来了今天迅猛发展的深度学习(deep learning)。值得一提的是，2006年这一时间点对于深度学习来说绝非起点而更像是复兴。

神经网络一词源自生物科学，它试图模拟大脑学习新事物的过程，由此衍生出来的人工神经网络就是一种模仿生物神经网络的运算结构，其基本构成是相互连接的简单计算单元，这些单元也可以简称为神经元。

真正意义上的“人工神经元”始于Frank Rosenblatt的感知机，但它建立在更早的神经学领域的研究成果上。

1943年，受到生物神经学的启发，神经生物学家Warren McCulloch和数学家Walter Pitts提出了最早的人工神经元 -- M-P神经元模型。

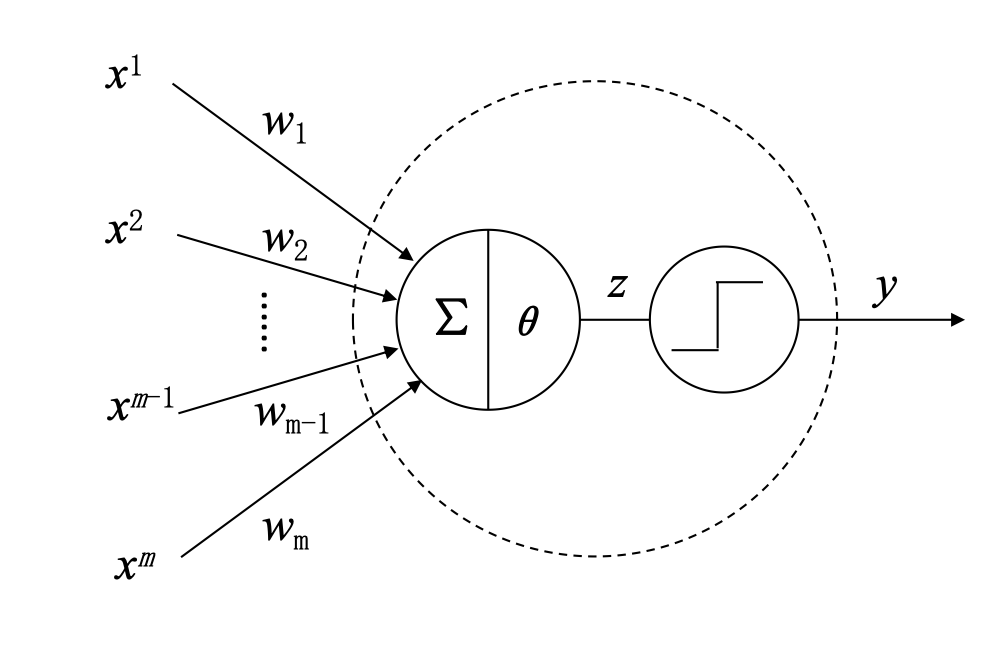
这一模型主要包括：

输入和权重：模型接收多个输入，每个输入对应一个权重，代表输入的重要性；
激活函数：模型使用一个激活函数，通常是阶跃函数；
二进制输出：输出是二进制的（1或0），分别对应激活或非激活状态。

M-P神经元模型虽然简单，但在理论上证明只要具备适当的权重和结构，可以实现任何布尔逻辑功能。这为后来的神经网络奠定了基础。

【笔记补充】输入信号 $\mathbf{x} :x_1,x_2,...x_n$ ，与之对应的权重 $\mathbf w: w_1, w_2,...w_n$ ，信号经过加权和计算: $x_1w_1+x_2w_2...x_nw_n$，与一个阈值 $\theta$ 相比较，之后通过激活函数，神经元会被激活（继续向后传递信号）或者不被激活（不继续传递信号）。如果被激活，输出的信号将会继续传递给下一个神经元。为了方便计算，“与阈值相比较”的过程将被抽象为更清晰的数学模型，即使用偏置(bias)的概念 $wx+b, \quad b\equiv -\text{threshold}$ , 数值上，偏置就等同于负的阈值。偏置可以理解为神经元被激活的容易程度，偏置大，意味着神经元很容易被激活。

1949年，生物学家Donald Hebb提出了神经心理学理论，其理论认为，在同一时间被激发的不同神经元之间的联系会被强化，神经网络的学习过程发生在神经元之间的突触部位，突触的连结强度与其连接的两个神经元的活性之和成正比。最典型的例子就是著名的巴甫洛夫条件反射实验。受到神经心理学的启发，关于人工神经网络的研究开始向模拟人类学习能力、使其可以通过算法调整权值的方向探索。

1957年，心理学家Frank Rosenblatt提出了感知机 perceptron 模型，它由两层神经元组成，输入层接收外界信号（但不进行计算），输出层就是上面的M-P神经元。感知机是神经网络的起源。神经网络作为机器学习中的算法模型，广泛应用于许多不同类型的问题，而在分类问题中表现尤其出色。
感知机通过有标记的数据训练确定合理的权重向量 $\mathbf w$ 。Rosenblatt提出了一个简单的参数更新方案，每一步的参数调整用一个微小变化 $\Delta w $ 来更新权值（参考式1.9），这种思路的核心就是上一章中已提到的梯度下降法：
$$ \Delta w = \eta (y-\hat{y})x_i \qquad \qquad (式2.1)$$
与上一章中的公式类似，$y$ 是训练数据的标记，$\hat{y}$ 是感知机的输出，$\eta$ 是一个0～1之间的小数，表示学习率。感知机的训练过程从事先设定的随机参数开始（事先人为设定好的参数成为超参数），当预测值与标记值不同时，根据更新规则调整参数。利用训练数据，不断重复这个过程，直到模型能够正确预测出全部数据。

感知机是第一个用算法精确定义的神经网络模型，而且实现了一个二元分类器。它最大的特征就是能够自动调整权值，因此真正具备了学习的能力。尽管单个感知机有局限性，只能实现线性分类，但感知机的灵活与强大正是在于它可以几乎无限制的叠加，从而解决复杂的逻辑问题。实际上，通过感知机网络，我们可以解决任意逻辑问题。
理论上，任何线性不可分的问题，无论有多复杂，通过无限次的增加直线，可以无限逼近实际曲线。

单层感知机与多层感知机 机器学习领域有诸多易于混淆的概念，多层感知机便是一例。按照严格的定义，感知机即所谓的单层神经网络，没有中间的隐藏层，它的输出是二元的。多层感知机一般来讲，意味着基础的前馈神经网络，使用其他形式的激活函数（而非二元输出），因此，最好避免使用这一说法。

2. 神经网络结构

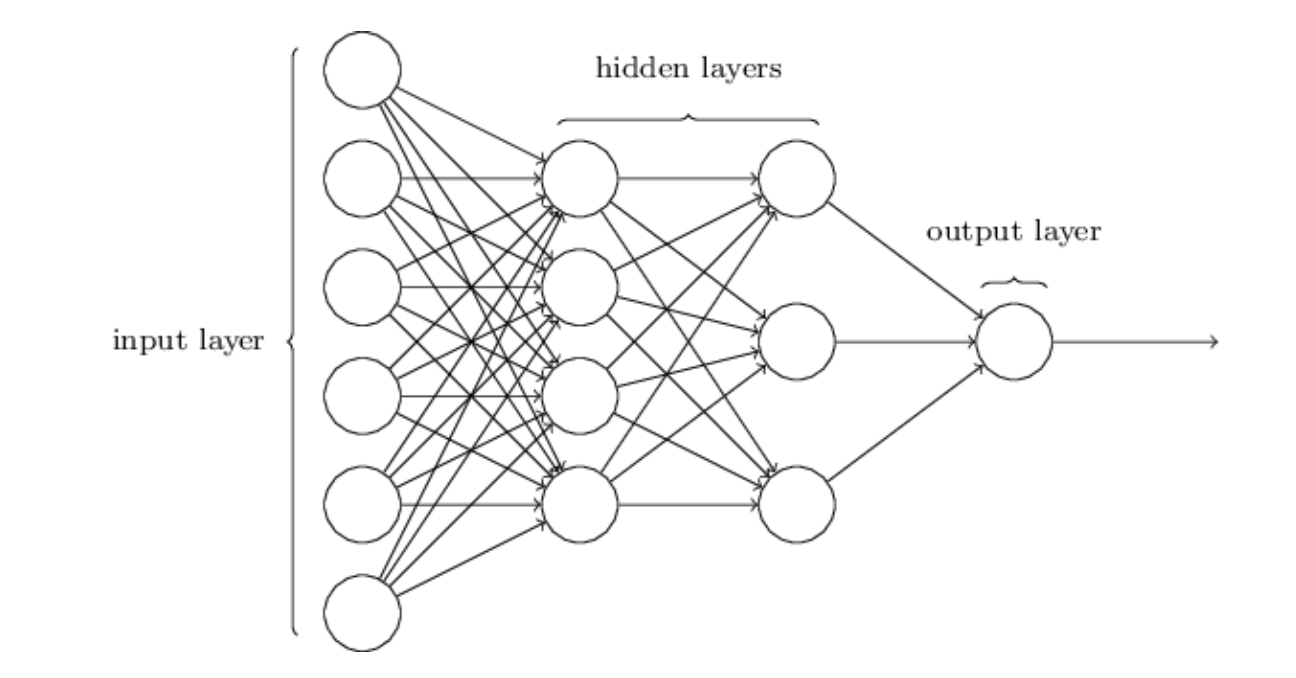
神经网络的结构简单来说就是输入层、隐藏层、输出层这三大板块。“隐藏”这个说法没有什么特殊含义，就只是区别于输入、输出的中间层，中间可以是一层或多层。

一个完整的神经网络流程可以大致抽象为下图：

具体到神经元的层面，假设一个有两个输入、两个输出的神经网络，它的信号传递过程大概如下图：

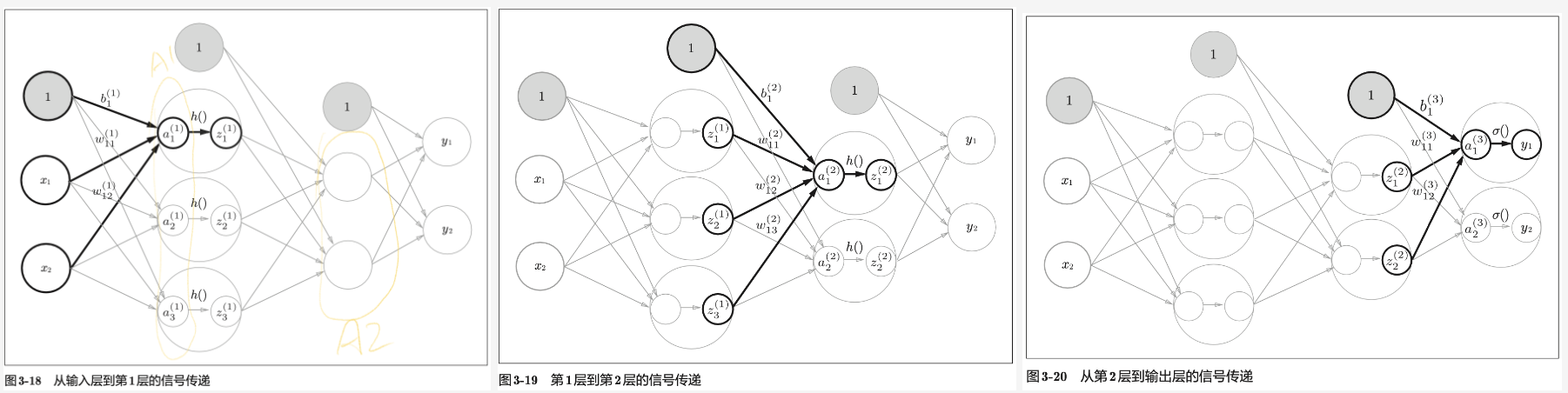
输入层：输入信号，不进行运算。因此这一层一般不计入神经网络层数的计算。图2.4是一个三层神经网络。
隐藏层神经元：首先计算 $a=wx+b$，这一过程也称“仿射变换”，即一次加权、一次平移。将a经过激活函数(图中 $h(x)$ 代表隐藏层函数）得到z，z作为下一层的输入进行与之前重复步骤的计算。图2.4选用的是具有两个中间层的神经网络结构，所以，重复了一次同样的计算。
输出层：最后，经过输出函数（用于输出层的另一种激活函数）得到最后的输出。

注意到隐藏层的神经元实际上包括了两项计算，首先是仿射变换，之后是激活函数。

3. 激活函数

神经元中的计算实际上分为两步，这是因为，简单的加权和计算出的结果仍然是原输入信号的线性组合，并不能解决更复杂的问题。在第一步线性计算完成后，得到的结果再经过非线性的激活函数得到输出，这样神经网络就有了无限逼近复杂函数的可能性。激活函数需要具备的一个重要数学特征是：连续可导，因为我们需要用梯度下降法不断求导、寻找最小值。

神经网络在发展初期主要使用典型的sigmoid函数——对数几率函数作为激活函数，在上一章中已提及（参考式1.13）。而sigmoid并非唯一的激活函数，常用的有如下几种：

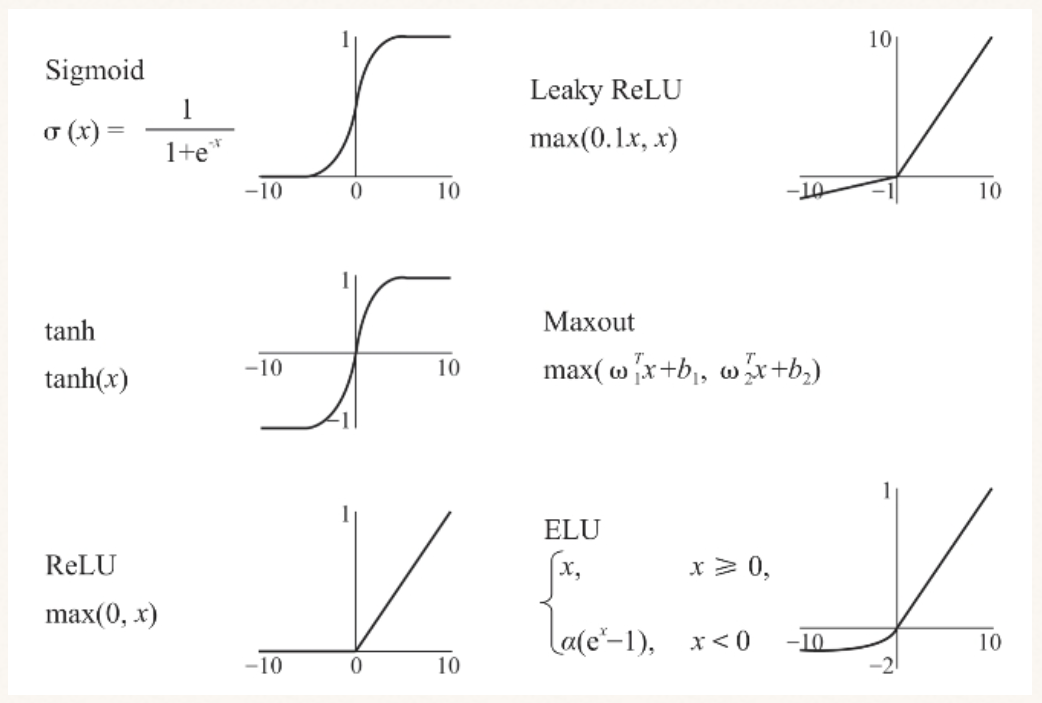
本节中，按照大多数神经网络书籍的习惯，使用z作为激活函数的变量。

Sigmoid

从sigmoid函数图像可以看到，当输入在0附近时，函数曲线接近线性，输出随着输入的增加而增加。但在取值的两端，即输入接近正负无穷大时，函数的导数几乎为零。使用sigmoid作为神经网络隐藏层的激活函数符合生物神经元的原理，当输入值较小时，神经元处于被抑制状态，而当输入值超过某个设定的阈值后，神经元被激活，并且输出值随输入值递增。由于它将输入值转换为了0～1之间的输出及其曲线特性，它的输出可以直接作为概率，因此在分类问题中常使用sigmoid。
sigmoid的缺陷：sigmoid的输出被限制在0～1之间，而非以0为中心。在神经网络中，每一层的输出都是下一层的输入，经过sigmoid函数后，后一层的输入相当于被偏移了。当我们利用梯度法，收敛速度可能因此变慢。改善这一问题的方式是用双曲正切函数Tanh替代sigmoid（图2.5）。

Tanh

$$ y=\frac{\sinh z}{\cosh z}=\frac{e^z-e^{-z}}{e^z+e^{-z}} \qquad (式2.2)$$
它的形状类似sigmoid，输出在-1～1之间。

Sigmoid和Tanh都有些复杂，需要进行幂运算，会增加神经网络的计算量和训练时间。另外它们的导函数都会有梯度消失的问题。

ReLU

现在比较常用的是 ReLU(Rectified Linear Unit 修正线性单元)函数，它常出现在卷积神经网络和其他一些深度神经网络模型中。ReLU的定义如下：
$$ y\equiv \begin{cases}
z & (z>0) \
0 & (z\leq0) \
\end{cases} \qquad \qquad $$
简单来说，ReLU函数是在0和输入之间取最大值。ReLU也符合生物学规律，当神经元接收到的输入小于0（或设定的阈值）时，神经元处于抑制状态。当输入一旦超过阈值，神经元被激活，并且输出相应的输入值（神经元兴奋程度随输入信号递增）。
ReLU函数相比前两种激活函数，在数学计算上很简单，计算速度也更快。，当输入大于阈值时，ReLU的导数恒等于1，这缓解了梯度消失问题。
它的缺点在于其输出同样不是以0为均值的，并且输入小于阈值时，输出为0，梯度为0，神经元完全被抑制，参数将无法更新，以之后的训练中永远无法再次激活。
针对这一问题产生了ReLU的改进版——Leaky-ReLU(图2.5)。

Leaky-ReLU

$$ y\equiv \begin{cases}
z & (z\ge 0) \
\frac{z}{a} & (z<0) \ \end{cases} \quad c\in (1,+\infty) \qquad $$ a是一个大于1的实数。
顾名思义，这个函数在输入小于0的那一侧有一点“leaking”，这一函数正是为了防止神经元被彻底抑制，因此使其保持一个较小的梯度用以持续更新参数。它的两个分段均为线性，运算速度也较快。不过式子中的实数a是一个超参数，需要人为设定和调整。

PReLU 和 RReLU

PReLU(Parameteric Rectified Linear Unit, 参数化修正线性单元)和RReLU(Randomized Leaky Rectified Linear Unit, 随机纠正线性单元)是另外两种ReLU的改进版。
$$ y\equiv \begin{cases}
z & (z\ge 0) \
\alpha z & (z<0) \ \end{cases} \quad c: 可训练参数 \qquad $$

RReLU随机纠正线性单元在训练阶段，负值部分的斜率是随机分配的；在训练阶段，负值的斜率是固定的（即训练阶段所有$\alpha$的平均值）。

使用激活函数的意义：在相同规模的神经网络下，使用合适的激活函数可以更高效的捕获到有用信息。

4. 误差反向传播算法

误差反向传播即BP(Backpropagation)，是神经网络训练中一种用于计算梯度的方式（而非神经网络的学习算法），这个梯度用于反馈给如“梯度下降”这种学习算法。神经网络中每一层的输出都是下一层的输入，每一层都面临计算损失函数梯度这一复杂任务。而BP是一种巧妙的计算导数的方式，利用求导算法中的“链式法则”，反向传播损失函数的梯度信息。从后往前遍历一遍神经网络，就可以计算出损失函数对网络中所有参数的梯度。所以，这一算法需要存储计算某些参数梯度时所需的任何中间变量（即偏导）。正向传播与反向传播可以大致表示为下图：

以具体函数为例，假设一个有三个自变量的简单函数：$f(x,y,z)=(x+y)\cdot z $ , 函数的计算过程可以用如下这种计算图表示出来。三个自变量分别取值-2，5，-4，它的正向计算过程为绿色数字部分，反向过程为红色数字：

首先完成正向计算过程，图中q用来表示x+y，最终输出-12。接下来从输出逆向返回。
$ dout=1 $，最外层的导为1；
$ dq=dout\cdot z=-4$，从导数的含义去理解，q的变化对于输出的影响是怎样的？乘法本质上是对被乘数进行scaling的过程，这就是为什么乘法进行反向传播时，乘数是互换的。
$ dz=dout\cdot q=3 $，同理，z的变化给输出带来的影响有多大，这个影响因子就是3。
$dx=-4,dy=-4 $，加法不影响导的变化，反向的过程直接将导继续原路送回即可。

再选一个《深度学习入门》书里比较经典的例子：

书中空出了反向传播的数值让读者自己去填写。这个计算可以从两个视角去想，一是直接按照已知的规律去填（黄字标注），二是实际去求导（蓝字部分），会发现最终结果是一致的。

训练神经网络时，前向传播与反向传播是相互依赖的。在初始化模型参数后，我们交替使用前向传播和反向传播，利用反向传播给出的梯度来更新模型参数。在这一过程中，需要存储中间值直到反向传播完成，这意味着训练模型需要更多的内存。

到此，本文已经涵盖了机器学习及神经网络所需的基础理论（包括数学公式的含义、计算原理）。在此基础上，我们可以比较轻松的进入更进一步的深度学习领域中，并用代码去实现神经网络的训练。