本课程是MITx在线数学课之一,是系列课程XSeries in 18.03x Differential Equations的第一个,也是学习后续高阶课的必修基础课,名为Introduction to Differential Equation 代号18.031x。整个系列未看到中文版。课程由来自麻省理工、普林斯顿等大学的多位教授、研究人员设计制作, 是一套非常棒的课程,内容丰满、制作精良。18.031x共有五个单元。本系列博客是经过我自己翻译后的中文笔记。
$$ \Large Unit\ 1:\ Modeling\ and\ first\ order\ ODEs $$
lecture 1 Modeling
ODE example 1:
假设你有一个储蓄账户,每天都在滚利,你频繁地存入和取出(利息的增长和存取状态都假定成一个连续的现金流状态,即假定成一个连续函数,而非离散数据)。写一个能够表达账户余额与各变量常量等之间关系的ODE。
首先,将所有涉及到的关系量及其单位标注出来。
P:初始值(dollars)
t:账户开启后经过的时间(years)
x:余额(dollars)
I:利率($year^-1$) (如4%/年)
q:净存入率(dollars/year)
这里t是独立变量,P是常数,x、I、q是关于t的函数。
在一个时间段内[t,t+dt],(dt代表微分,也可以写成$t+\Delta{t}$, 然后$\Delta{t}$无限趋近0), 当dt无限小:每一美金赚得利息=$I(t)dt$, 所赚利息=$I(t)x(t)dt$ , 存进账户的钱=$q(t)dt$
于是有:$dx=$ 余额变化 $=I(t)x(t)dt+q(t)dt$
$\frac{dx}{dt}=I(t)x(t)+q(t)$
(注意检查两边的单位是否一致)。关系式表达出来后,是考虑初始值,$x(0)=P$. 因此可以写成完整的ODE: $x'=I(t)x+q(t), x(0)=P $
lecture 2 Solving first-order ODEs
变量分离法
一阶常微分方程的基本求解方法。
$\clubsuit $ 求解$y'-2ty=0$
首先确定它是一个一阶常微分方程。
$$ \frac{dy}{dt}-2ty=0 \ \Rightarrow \ \frac{dy}{dt}=2ty \ \Rightarrow \ \int\frac{1}{y} dy=\int2tdt $$
$$ ln|y|=t^2+C \ \Rightarrow \ |y|=e^{t^2+C}=Ce^{t^2} $$
(C is arbitrary) 常量C是任何可能的实数,可以直接去掉绝对值符号了。由于上面有一步除以y的计算,因此要检查y=0的情况。事实上当C=0就可以实现,因此可以放心的说,C是任意实数。那么也就是说,原微分方程的一般解为:$ y=Ce^{t^2}$ (C为任意实数)
将解带入原微分方程,可得恒等式。
System and signal
描述微分方程所表达的关系,常用到“系统与信号”的概念。如前面的储蓄账户例子,其表达式可以重写成$x'-I(t)x=q(t)$,其中q是一个“输入信号”,银行是那个系统,x是输出信号(或系统响应)。
应用题目1: 非洲大羚羊
某个非洲政府正在试图制定针对特定狩猎区内羚羊狩猎的良好政策。他们使用以下模型:羚羊种群的自然增长率为k(每年),k为正数,并且假设存在恒定的每年 a 只羚羊的捕猎率。(注:原题中,k是无单位的——k/year, 而a是常数——a oryxes/year, 所以k是一个百分比,也就是一般的RNI的概念——一定时间段内的实际增长,出生人口与死亡人口的差值占比初始总人口的比例)
1, modeling the population
用k,a和x写一个微分方程来模拟大羚羊的数量变化关系,可以表示为:
$$ \frac{dx}{dt}=xk-a $$
2, Signals and systems
如果用信号与系统的语言去描述,这里的输入信号就是a——由政府控制的捕猎率,系统响应(输出结果)就是x,羚羊数量。
3, No hunters?
假设a=0,也就是没有捕猎的情况,在什么时间,种群数量翻番?用k来表示。
$ \frac{dx}{dt}=x(t)k(t) $
这就是典型的增长模型,其一般解为$Ce^{kt}$,C为初始值,所以有时候也写成$x_0$,即 $ x=x_0e^{kt} $
数量翻倍指的是数量达到初始值的2倍: $ x_0e^{kt}=2x_0 $
可以算出 $t=ln(2)/k$
另外还有一个问题,1/k年后,数量增长了多少倍?这时t=1/k,把它带入到前面得出的x的函数中,
$ x=x_0e^{k*\frac{1}{k}} $ 因此增长了e倍,也就是说增长倍数是e。
$ \bigstar $ 4, General solution
找到前面得到的这个ODE( $\frac{dx}{dt}=xk-a$ )的一般解,用k,a,t和初始值$x_0$.

最终结果为: $$ x=\frac{(kx_0-a)e^{kt}+a}{k} $$
5, constant solution
找到一个常数解。当x的变化率为零时,得到常数解。因此这个常数解可以表示为:$x=\frac{a}{k}$
6, solution behaviour
令k=0.2, a=20,画出常数解,再分别画出初始值在其上和其下的一般解各一个。
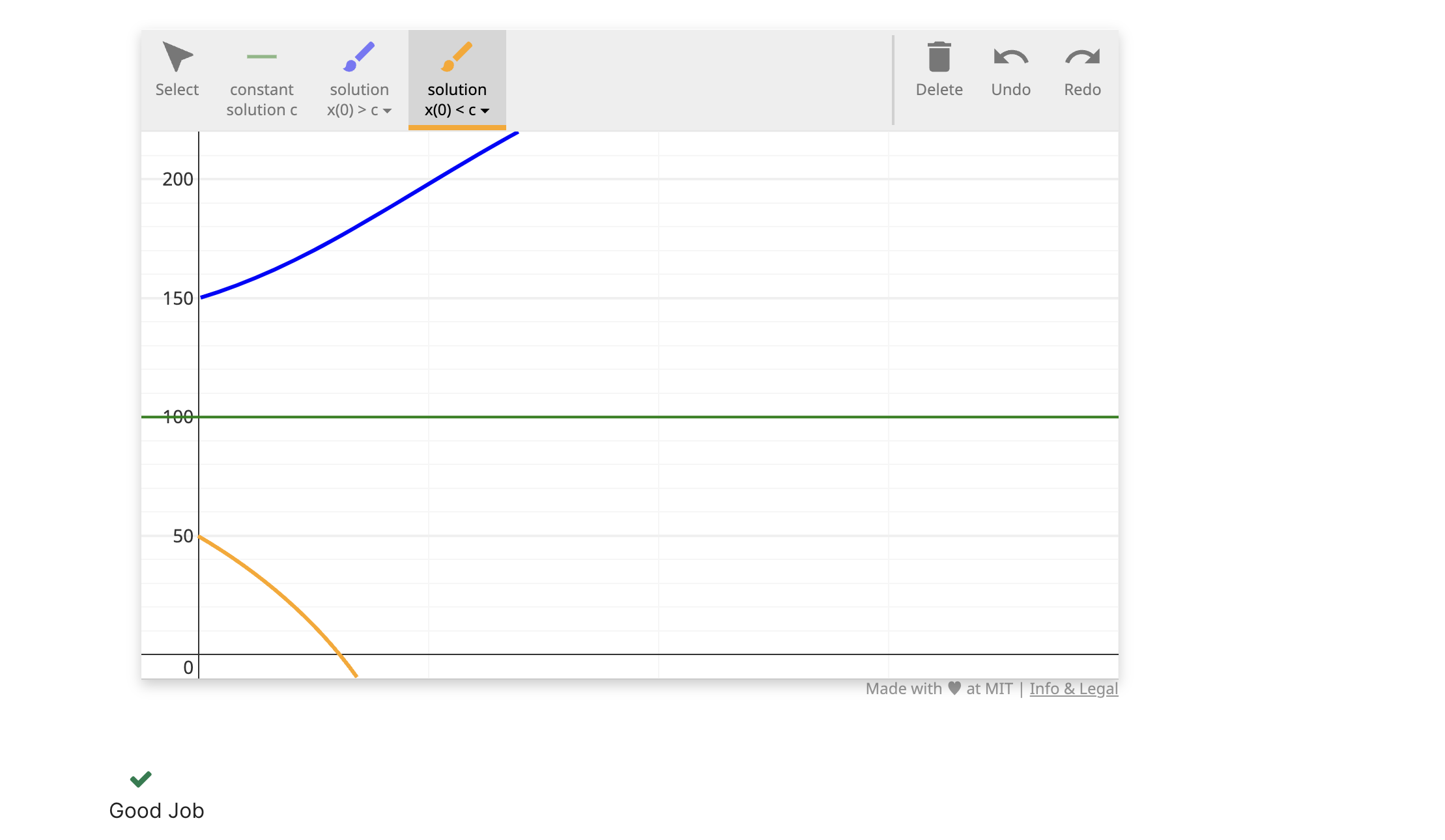
注意到当初始值在平衡线以下时,这个模型会在某个时间点后变得没有实际意义,因为它在计算负数值了,那也就意味着这个地区的羚羊被清除没了。在这种情况下,指数部分的系数$kx_0-a$为负,所以曲线朝下走。计算出特定的那个时间点$t_e$,在这个时间点后,这个地区的羚羊全部消失。 另初始值为$x_0$ (从上图容易看出,这时候的初始值是小于100的),用k,a,x_0表示这个特定时间点。
这种情况就是x值为零的时候,即
$$(kx_0-a)e^{kt}=-a \ \Rightarrow \ e^{kt}=\frac{a}{a-kx_0} \ \Rightarrow \ t_e=\frac{1}{k}ln(\frac{a}{a-kx_0}) $$
一阶线性ODE
一阶线性常微分方程的标准式: $$ y'+p(t)y=q(t) $$
q(t)为零时,即为齐次方程。$ y'+p(t)y=0$
一阶齐次线性常微分方程的一般解为: $$ y=Ce^{-p(t)} $$ C由初始状态确定。
Variation of Parameters 非齐次求解
Variation of Parameters 方法是一种以猜测的形式寻找特解的方法。它通过假设特解具有特定的形式,并使用可变的参数来确定这些特解。
【参数变化法】 求解$ty'+2y=t^5$
$\bullet$ step 1, 首先,求解该齐次方程的对应齐次解。这通常使用齐次线性微分方程的常规方法,如特征方程或特解公式。
其关联齐次方程为$ty'+2y=0$ 用变量分离可得: $ y=Ce^{-2lnt}=C(e^{lnt})^{-2}=Ct^{-2} $
C可以为任意值,这里我们选择一个最简单的非零解,C为1的时候,$y_h=t^{-2} $(注意,C为零的时候,有一个特殊解,即y=0)。 $y_h$表示homogenous的一个解。
$\bullet$ step 2, 对于非齐次方程的特解,我们假设特解可以表示为一个特殊的形式,包含待定的参数,这个参数通常是自变量的函数,需要从微分方程中解出。
求解非齐次方程的特解:为了求解非齐次方程的特解,我们需要猜测一个特定形式的解,并将其代入原方程。猜测的形式通常与非齐次项的形式相关。常见的特解形式包括常数函数、多项式、指数函数、三角函数等。
引入待定函数u(t) 假设$y=u(t)t^{-2}$, u(t)是一个待定函数。将y带入到原方程左侧:
$$ ty'+2y=t(u't^{-2}+u(-2t^{-3}))+2ut^{-2}=t^{-1}u' $$
(带入过程中必然会有一对消除项,如果没有运算到消除过程,说明有计算错误。)
$\bullet $ step 3, 将这个猜测的特解带入非齐次方程,求解出参数的导数,进而求出u的一般解。
$$ t^{-1}u'=t^5 \ \Rightarrow \ u'=t^6 \ \Rightarrow \ u=\frac{t^7}{7}+C $$
所以原方程的一般解为:
$$ y=ut^{-2}=(\frac{t^7}{7}+C)t^{-2}=\frac{t^5}{7}+Ct^{-2} $$
第二步中之所以采用u(t)而非常数,是因为我们明确知道使用常数项代回原方程后,两边无法画等号。毕竟$Cy_h$是我们求得的齐次方程的解,也就是等号右边将为0而非原方程的q(t). 于是我们尝试一个未知函数u,一个能够得到得到q(t)的u。这就是为什么称之为“变参数法”。
"变参数法"(variation of parameters)是一种求解非齐次线性微分方程的特解的方法。它假设特解可以表示为齐次方程通解的线性组合,其中系数是关于自变量的函数。变参数法的基本思想是通过引入待定函数来求解非齐次方程的特解。这种方法的优点是适用于一般形式的非齐次线性微分方程,但需要进行一些代数计算和求导操作。在具体应用中,选择合适的齐次解和待定函数形式对于求解特解的成功非常重要。
Variation of Parameters 例题
求解这个给出了初始值的ODE:
$$ \dot{y}+ty=t; \ \ \ \ y(0)=3 $$

Superposition 叠加原理
$\clubsuit$ 对于一个线性常微分方程,如果我们已经知道了它的两个解,那么它们的线性组合也是该方程的解。

-
叠加原理的使用场合包括:
1, 求解齐次方程:对于齐次线性常微分方程 L[y] = 0,我们可以找到两个线性无关的解,然后利用叠加原理得到该方程的通解。
2, 求解非齐次方程:对于非齐次线性常微分方程 L[y] = g(t),其中 g(t) 是已知函数,我们可以先求解对应的齐次方程 L[y] = 0 的通解,再找到一个特解 y_p(t)。然后利用叠加原理,将齐次方程的通解和特解相加,得到非齐次方程的通解。 -
叠加原理应用到非齐次ODE的求解
例:已知 $ct^{-2}$ 是齐次微分方程 $t\dot{y}+2y=0$ 的通解;$t^5/7$是非齐次微分方程 $t\dot{y}+2y=t^5$ 的一个特解;那么 $t\dot{y}+2y=t^5$ 的通解是什么?
答:$t^5/7+ct^{-2}$
也就是说,找到相关齐次的通解,再只需要找到一个非齐次的特解,就可以构造出这个非齐次ODE的通解。
$ y_i = y_p + y_h $ 非齐次方程的特解加上齐次方程的一般解得到非齐次的所有解。 -
叠加原理只适用于线性微分方程,即方程中的未知函数及其导数的次数均为一次,并且满足线性关系。非线性微分方程则不适用叠加原理,其求解方法通常较为复杂。
对于任意一个c,$t^5/7+ct^{-2}$ 将会给到等号右边为 $0+t^5=t^5$ 的非齐次ODE的解。那为什么这个式子覆盖全部解?因为这个过程反过来依然成立,给到任意一个非齐次的特解,我们都可以减掉$t^5/7$得到齐次的通解。 叠加原理是相加的过程,减法也一样,而右侧减掉的过程$t^5-t^5=0$,相应的解也一样进行减法操作,并得到齐次方程的通解。
积分因子解非齐次方程
另一种求解非齐次ODE的方法是 $ \large integrating\ factor $。

$\diamondsuit$ 例题:$ xy'-y=x^3 $
-
step 0, 整理为标准形式。
$$ y'-\frac{y}{x}=x^2 \ \Rightarrow \ p=-\frac{1}{x} $$ -
step 1, 找到积分因子u。
$$ u=e^{\int(-\frac{1}{x})dx}=e^{-ln(x)}=(e^{ln(x)})^{-1}=x^{-1}=\frac{1}{x} $$ -
step 2, 将因子乘到ODE两边(整理后的标准式)。
$$ \frac{1}{x}y'-\frac{y}{x}\cdot \frac{1}{x}=x^2 \cdot \frac{1}{x} \ \Rightarrow \
\frac{1}{x}y'-\frac{1}{x^2}y=x$$
等式的左边应该就是 $\frac{1}{x}y$ 的导函数,这里最好检查一下,求导后是否刚好为左边的式子。 -
step 3, 两边积分。
$$ \int{\left(\frac{1}{x}y\right)'} dx=\int{x} dx \ \ \Rightarrow \ \ \frac{1}{x}y=\frac{x^2}{2}+c $$
$$ y=\frac{x^3}{2}+cx $$
线性ODE习题
考察这个线性ODE: $ \large y'-(tanx)y=1 $
- 找到满足其相关齐次方程的解$y_h$,且 $ y_h(0)=1 $:
求解 $ y'-(tanx)y=0 $,
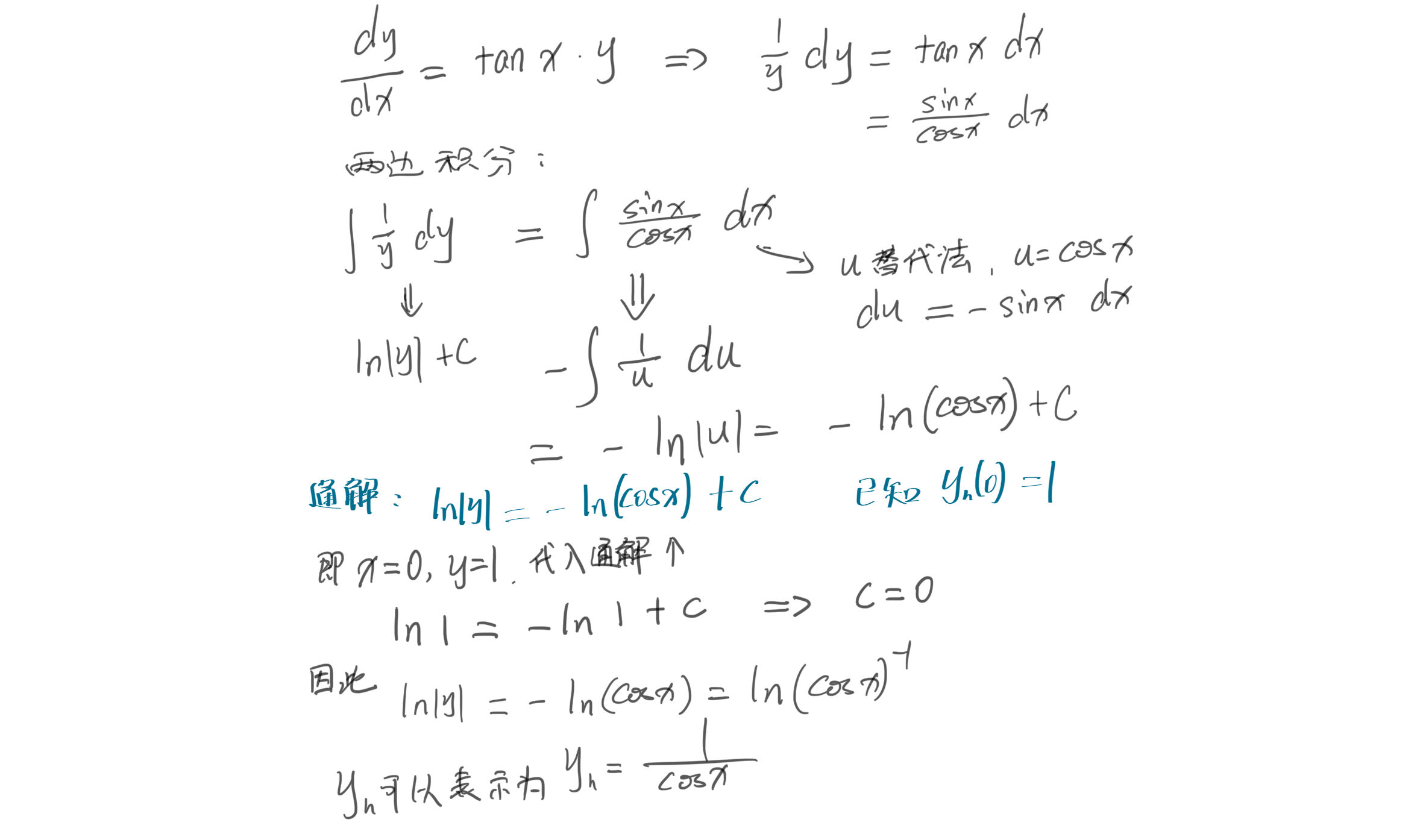
$$ y_h=\frac{1}{cosx} $$
-
利用$y_h$找到$u(x)$使得$y=u(x)\cdot y_h$ 是原微分方程的一个解。
assume $ y=u(x)\frac{1}{cosx} $ (简写为 $\frac{u}{cosx}$), 代回原ODE(此时的y为分数形式,求导函数要用到quotient rule):
$$ y'-(tanx)y=\frac{u'cosx+usin(x)}{cos^2x}-tanx\frac{u}{cosx}=\frac{u'}{cosx}=1 $$
$$ 因此 \ \ \ u'=cosx \ \Rightarrow \ u=sinx+c $$ -
求一般解, 用$y_0$表示初始值$y(0)$
$$ y=\frac{sinx+c}{cosx}+\frac{1}{cosx}, (superposition \ \ principal \ \ y_i = y_p + y_h) $$
$$ y_0=c+1,\ c=y_0 - 1 $$
finally, $$ y=\frac{sinx+y_0-1}{cosx}+\frac{1}{cosx} $$
应用题目2: 为海鱼混合盐水
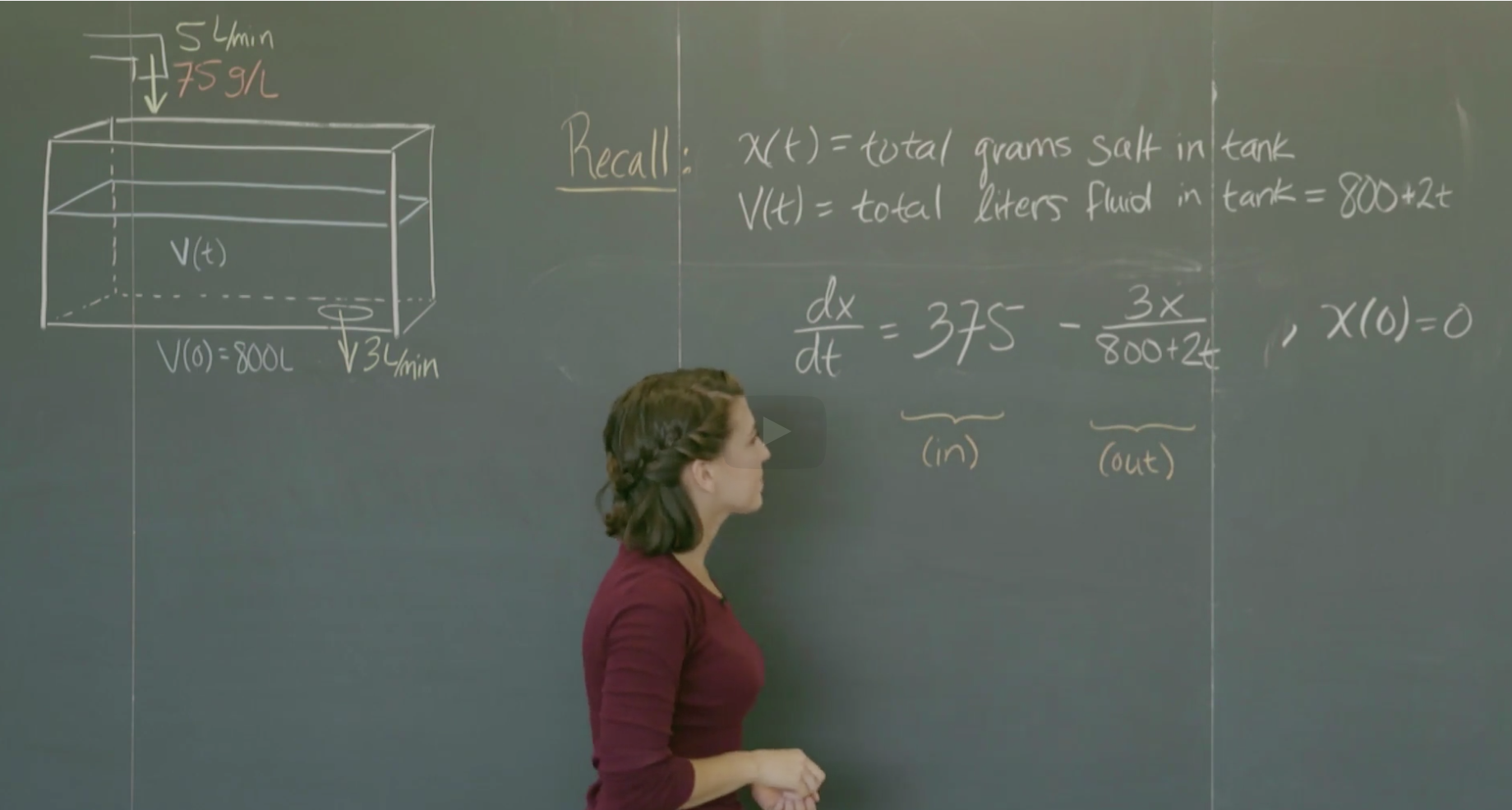
原题背景:目前对盐水的要求是34g/L的浓度。现有浓度为75g/L的盐水,以每分钟5L的速度灌入一个水箱中,水箱最开始装有800L的纯水并且水箱底部有一个出水口,以每分钟3L的速率向外流出,所以每分钟净流入2L的液体。盐量x和水箱中的液体总量V都是关于时间t的函数。盐度可以表示为 $conc=\frac{x(t)}{V(t)} $,由于分子分母都随着时间变化,这个关系表示起来很复杂。现在我们可以只考虑x(t)的变化率, $\frac{dx}{dt}=(rate \ in)-(rate \ out) $ 。每分钟灌入的5L盐水浓度为75g/L,所以盐的灌入率: $ rate in=75g/L \cdot 5L/min = 375g/min $;同理,盐的流出率应该是当下时间点的水箱里的盐度乘以流出速率,显然当下某个时间点,水箱的盐度是在变化着的、不确定的(前提假定盐水是立刻混合的,水箱中的水每一处的盐度是均匀的),那么盐的流出率可以表示为: $ rate out=\left(\frac{x(t)}{V(t)}g/L \right) \left( 3L/min \right) $, 水箱中的总液体量 $ V(t)=800+(5-3)t=800+2t $, 由此便可以写出x变化率的ODE:$$ \frac{dx}{dt}=375-\frac{3x}{800+2t} $$
现在考虑一个可能的终极状态,即很长很长时间以后,水箱中的浓度将等同于注入盐水的浓度(盐水一直注入,水箱一直外流),这便是最终的“稳态”。可以表示为:
$$ conc=\frac{x(t)}{V(t)}= \frac{x(t)}{800+2t}=75\ \ (for\ \ large\ \ t) $$
用这个明确的关系可以直接推导出一个“稳态” long-term prediction:
$ x(t)\approx75(800+2t)=60000+150t $, 这实际上就是一个求极限的结果,也就是$t无限大时所得的极值$。
海鱼的需求盐度是34,但这个长期的预测模型告诉我们盐度最终将达到75,这远高于需求值。需要求解完整的方程,并且找到发生变化的时间点。
解微分方程
原来的ODE,把它变成标准的$ x'+p(t)x=q(t)$的形式后就是:
$$ \frac{dx}{dt}+\frac{3x}{800+2t}=375 $$
显然这是一个非齐次ODE,运用associate homogeneous等分步骤求解。
$\bullet$ step 1 解相关齐次方程:
$ ln(x)=-\frac{3}{2}ln(400+t)+c \Rightarrow x=ce^{-\frac{3}{2}ln(400+t)} $
选择最简单系数的情况,抹掉c,从而得到一个好用的齐次解: $ x_h=(400+t)^{-\frac{3}{2}} $
$\bullet$ step 2 参数变化法,引入u(t):
$x=u(t)x_h(t), \ x'=u'x_h+ux_h'=u'(400+t)^{-\frac{3}{2}}+u(-\frac{3}{2})(400+t)^{-\frac{5}{2}} $
带入原微分方程中:
$ u'(400+t)^{-\frac{3}{2}}+u(-\frac{3}{2})(400+t)^{-\frac{5}{2}}+\frac{3u(400+t)^{-\frac{3}{2}}}{2(400+t)}=u'(400+t)^{-\frac{3}{2}}=375 $,
$ u'=375(400+t)^{\frac{3}{2}} $,
$ u=375(\frac{2}{5})(400+t)^\frac{5}{2}+c=150(400+t)^\frac{5}{2}+c $
$\bullet$ step 3 将x表示出来(一般解):
$$ x(t)=u\cdot x_h=(150(400+t)^{\frac{5}{2}}+c)(400+t)^{-\frac{3}{2}}=60000+150t+\frac{c}{(400+t)^\frac{3}{2}} $$
$\bullet$ step 4 带入initial condition
最初的盐量为0,水箱中只有纯水。带入 $ x(0)=0 $
得到 $ c=-4.8 \cdot 10^8 $, 最终得到:
$$ x(t)=(60000+150t)-\left(\frac{4.8 \cdot 10^8}{(400+t)^\frac{3}{2}}\right) $$
注意到左侧的括号正是前面推导出的$长久稳定状态$的公式,实际上当t趋向无穷时,右边括号中的值就趋向0了,这部分正是短期状态的表达。
浓度变化
盐水浓度随时间发生怎样的变化?一直增长/减少还是时而增时而减。
已知的关系式 $ C(t)=\frac{x(t)}{V(t)} $
$$ \frac{dx}{dt}+\frac{3x}{V(t)}=375,\ V(t)=800+2t $$
考虑浓度的$\large 变化$, 就是要考察浓度C(t)的导函数的正负。根据quotient rule,
$$ C'=\frac{x'V-xV'}{V^2} $$
带入$ x'=375-3x/V,\ V'=2 $, 于是得到:
$$ C'=\frac{375V-5x}{V^2} $$
分母恒为正,只考虑分子的符号即可。V和x的表达式都已经求出来了,带入 $375V-5x$ :
$$ 375(800+2t)-5\left(60000+150t-\frac{4.8 \cdot 10^8}{(400+t)^\frac{3}{2}}\right)=5\left(\frac{4.8 \cdot 10^8}{(400+t)^\frac{3}{2}}\right) $$
整理后的式子恒为正,因此,盐水浓度一直在增长。
1800L的水箱是否够用?
假设水箱容量为1800L,在达到理想浓度34g/L之前,溶液是否会水满溢出?
由于$ V(t)=800+2t $, 达到1800L时的时间t为500,带回到浓度计算公式,
$$ C(500)=\frac{x(500)}{1800} $$
计算得出浓度大于34(约为65),所以不会过满溢出。
应用题目3: 被两个弹簧固定着的物体
一个质量为m的物体两端各由一个弹簧固定在左右两面墙上。物体假定在一个无摩擦的空气台面上。假定两个弹簧都符合Hooke定律,左边弹簧系数为k1,右边弹簧系数为k2,用x表示物体相对于中间均衡位置的位移,从均衡点往右的位移意味着x>0,从均衡点往左的位移x<0。利用牛顿第二定律写关于x(t)的微分方程。$ mx''=? $
有两股力作用于物体:
$ |F_L|=k_1|x|, |F_R|=k_2|x| $
x=0时,物体就是在均衡点。
x>0时,物体被向右移,左侧弹簧被拉伸并对物体产生向左的拉力,即(-x)的方向,这时左弹簧力为负;同时,右侧弹簧被压缩并对物体产生向左的推力,即也是(-x)方向,这时的右弹簧力同样为负。因此:
$ F_L=-k_1x,\ \ \ F_R=-k_2x $
x<0时,上式同样适用。
根据牛顿第二定律,合力为质量与加速度的乘积:
$$ mx''=-k_1x-k_2x=-(k_1+k_2)x $$
应用题目4: 废弃屋加热
(1) Temperature of an unheated house
一个废弃屋的温度$T=T(t)$, 表示在t小时的华氏度。如果户外温度为40(波士顿地区的秋季平均气温),这个房间经过24小时,会从70华氏度降到55华氏度。用牛顿冷却定律(物体的冷却速率与其和外部气温的温差成比例关系)写出微分方程。
用k表示正系数: $ \dot{T} = k(40-T) $, 整理为标准式: $ \dot{T}+kT=40k $, 等式右边是个常数,意味着它有一个特解为 $y=40$ .
解这个微分方程,首先求解相关齐次方程: $ T_h=ce^{-kt} $
知道特解和齐次的一般解,可以利用叠加原理:
$$ T=40+ce^{-kt} $$
已知房间在24小时内会从70度降到55度,利用这些信息可以把k,c求出来:
$$ T(0)=70=40+ce^{-k\cdot 0}=40+c \ \Rightarrow \ c=30 $$
$$ T(24)=55=40+30e^{-k\cdot 24} \ \Rightarrow\ k=ln(2)/24 $$
因此:
$$ \dot{T}=\frac{ln(2)}{24}(40-T) $$
(2) Temperature of a heated house
有人买了这个房子后,打开了暖气,这时T的微分方程为:$ \dot{T}=k(40-T)+q $,考虑稳定状态(很长时间之后的状态)即 $ \lim\limits_{t \rightarrow \infty}T(t) $,用k和q来表达稳态的函数。
先整理标准式, $ \dot{T}+kT=40k+q $, 和上题类似,右边也是常数,有一个特解为 $ 40+\frac{q}{k} $(代回原式检查)。
一般解仍然利用叠加原理:
$$ T = 40+\frac{q}{k}+ce^{-kt} $$
当$ t\rightarrow \infty, e^{-kt} \rightarrow 0 $, 因此T的极值是$ 40+\frac{q}{k} $.
极限温度也就是稳态温度,其实就是一个常数解。
【注】极限情况应该可以通过合理预测推导,长时间后的状态是“无变化”,即$ \dot{T} $ 为零。那么就意味着原微分方程$ \dot{T} =k(40-T)+q=0 $
便可直接推导出结果。
(3) Energy efficiency
维持70度与维持55度所需的能效之比。所需能量就是上题中的q的值。70度的q值指的是每小时维持70度所需的加热温度,55度q值同理。
既然是“维持”某温度,这指的正是“稳态”温度。从上题已知稳态的式子,可以推算:
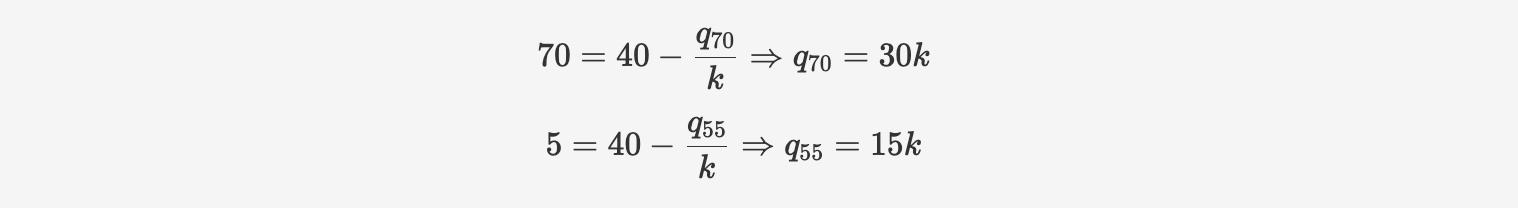
所以比值就是 $30k/15k=2$.
注意到参数 q 大致与供暖房屋所消耗的能量成正比,因此与每小时的费用也成正比。因此,将稳态温度从55提高到70会使每小时的费用翻倍。这并不令人惊讶,因为与室外温度的差异也翻倍了。真正令人惊讶的是,这个比例与常数 k 无关,常数 k 反映的是房屋的绝缘性能。但绝对费用却是与 k 成线性关系!
