♥ ♥ HTML导出版 ♥ ♥
[========]
Part I 初等物理(简谐振荡)
周期运动 Periodic motion
任何以等长的时间反复进行的运动都可称为周期运动。四种常见的周期运动,或许你在物理课上曾见到过:
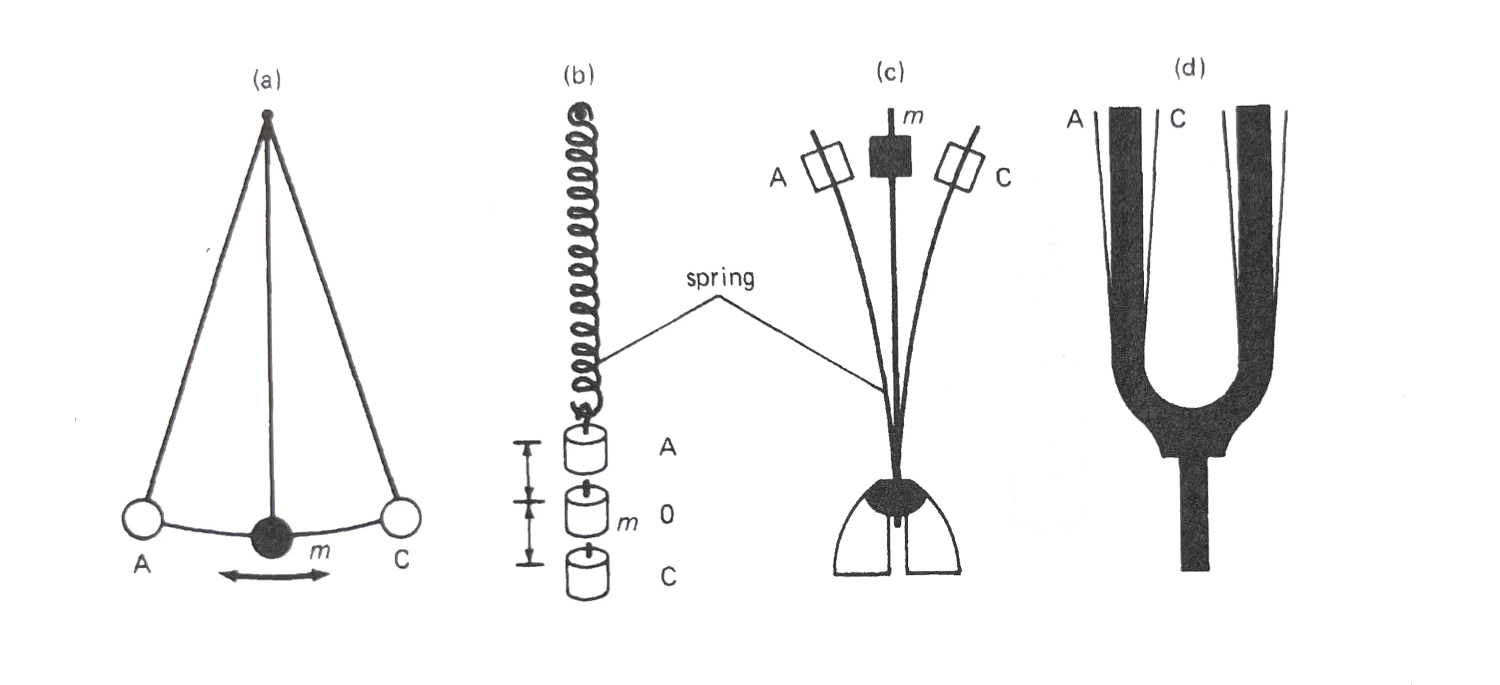
振动体不断地、重复地回归原点,单次振动就称为一个cycle, 可理解为一个来回、一个周期事件。
A. 简谐运动
在许许多多的工程领域中,最基本也最重要的研究对象当属简谐运动。
无论是不断来回伸缩的弹簧,还是左右均衡摆动的钟摆,这些熟悉的场景就是最典型的简谐运动simple harmonic motion。
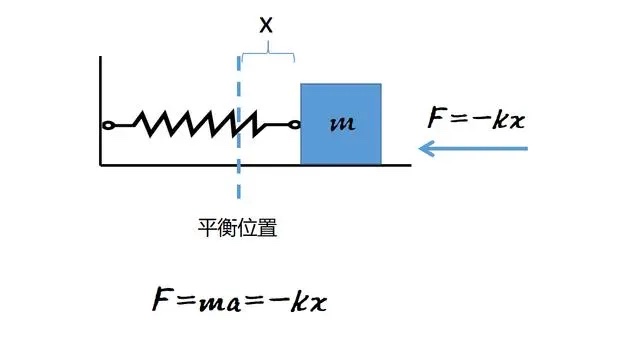
假设有个弹簧一端固定在墙上,另一端连接一个物块(有时也会用小车),当弹簧处于稳定状态(未被拉伸或压缩)、物块静止不动时,物块停住的位置称为平衡位置,从平衡位置往右或往左产生的位移,通常用x表示,它是关于时间的函数x(t)。设定在平衡位置右侧,位移为正,在左侧则为负。弹簧本身有弹力,它的弹性系数用 $k(N/m)$来表示,k为正数。默认不考虑摩擦力、空气阻力等。
使得这个系统成为振荡系统的关键就是弹簧带来的一种恢复力restoring force or returning force,这个恢复力有两大特征:
- 力的方向总是朝向平衡点
- 力的模与运动体的位移成正比
这样的系统遵循“胡克定律 Hooke's law”,对于上图所示的系统,不难看出,恢复力的方向总是与位移的方向相反,由此,这个力的关系被表示为:$ F_{spring}=-kx $。
$ \scriptsize 扩展:根据牛顿第二定律,合力等于质量与加速度的乘积\ F=ma,加速度a就是位移的二阶导数,由此可写出微分方程 m\ddot{x}+kx=0 $ .
这个系统的构成与基本关系了解到这即可。
所谓simple harmonic motion,simple指的是最简单、最基本的正弦波——sine或cosine,它是所有复杂波的根本构成,因此是最重要的研究对象。正弦曲线在x轴上下周期性来回,始终保持同样的步调。一个无摩擦的理想振荡系统所呈现的位移变化正符合正弦波,这种振荡便称为“简谐振荡 simple harmonic oscillation“。
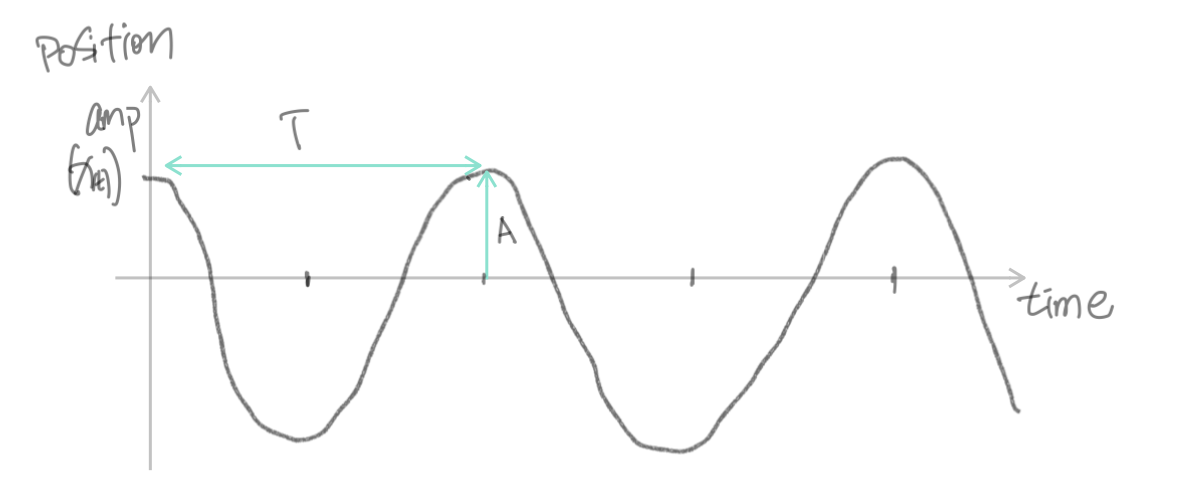
B. 振幅与周期
上图所示的系统中,物块左右摆动的位移有多大,也就是物块“偏离”平衡位置有多远,即是所谓的振幅 amplitude,体现在图像上,就是“波峰(或波谷)” 有多高。数学上,常用A来表示。
注意,位移是有正负的(矢量),振幅则是非负实数(标量)。
既然这个运动是循环往复的,它一定有周期,所谓周期 period,就是”走完一个完整来回,回归原位置、原状态所消耗的时间“,常用T来表示,它的单位当然是时间,比如秒、毫秒。物块从某一点出发,一个周期后,它将回到原来的出发点、回归原来的速度与方向(fully reset),之后是新一次一模一样的循环。
如果我们用弹簧系统的那个示意图去描绘物块一次又一次的运动,将会出现同样的位置上画了无数反复的路径,显然是画不清楚的,那么应如何表示物块的运动呢?答案正是完美的正弦曲线。
体现简谐振荡的正弦曲线图像,它的横轴是时间,纵轴表达振幅,某种程度上来说,你可以把它看成简谐运动在时间维上的展开。
前面的弹簧示意图是直接而原始的,它用简化的方式把我们眼中实际看到的物理存在用符号与线条表示出来。水平方向上,物块来回移动,然而到了正弦图像中,这个水平的轴被“翻转”到了纵向上,横轴变成了时间。
如果你从直接的物理示意图转换到正弦图像去理解每一点,可能会觉得拧巴,因为它被扭转了。其实,与其说“翻转”,莫不如说是新增了一个维度——时间。尽管它们看起来都是一张图,但前面的物理示意图,实际上只表达了一个维度的内容——位移,而通过使用坐标系,在两个坐标轴上完美表现了两个维度的数据。
C. 简谐振荡表达式
正弦型函数 sinusoidal function 是许多工程领域的重要基本函数,在不同的数学语境中它有不同的表达方式。在声学基础阶段,我们只需要了解它最常用的一种表达式,只用到简单的余弦函数,这种形式也被称为“振幅-相位”型表达式 Amplitude-Phase form。
$$ A\cos(\omega t) $$
三角函数 $\cos \theta$ 我们是熟悉的,从基础的 $\cos \theta$ 怎样一步步构建出上面那个表达式?
我们准备构建的是一个关于时间的函数,它的输出是物块的位移,因此函数名为 $x(t)$ .
a. 针对这个图像,显然它是一个余弦曲线,因此先把它写为 $\cos(t)$ ;
b. 余弦值的范围在[-1,1],但是我们需要的振幅不一定就是1,现在需要一个负责scaling的因子,于是得到 $A\cos(t)$ ;
现在这个函数已经可以表达上述曲线了,但是并不实用。我们已知余弦周期为 $2\pi$ ,现在最好回忆一下极坐标形式。
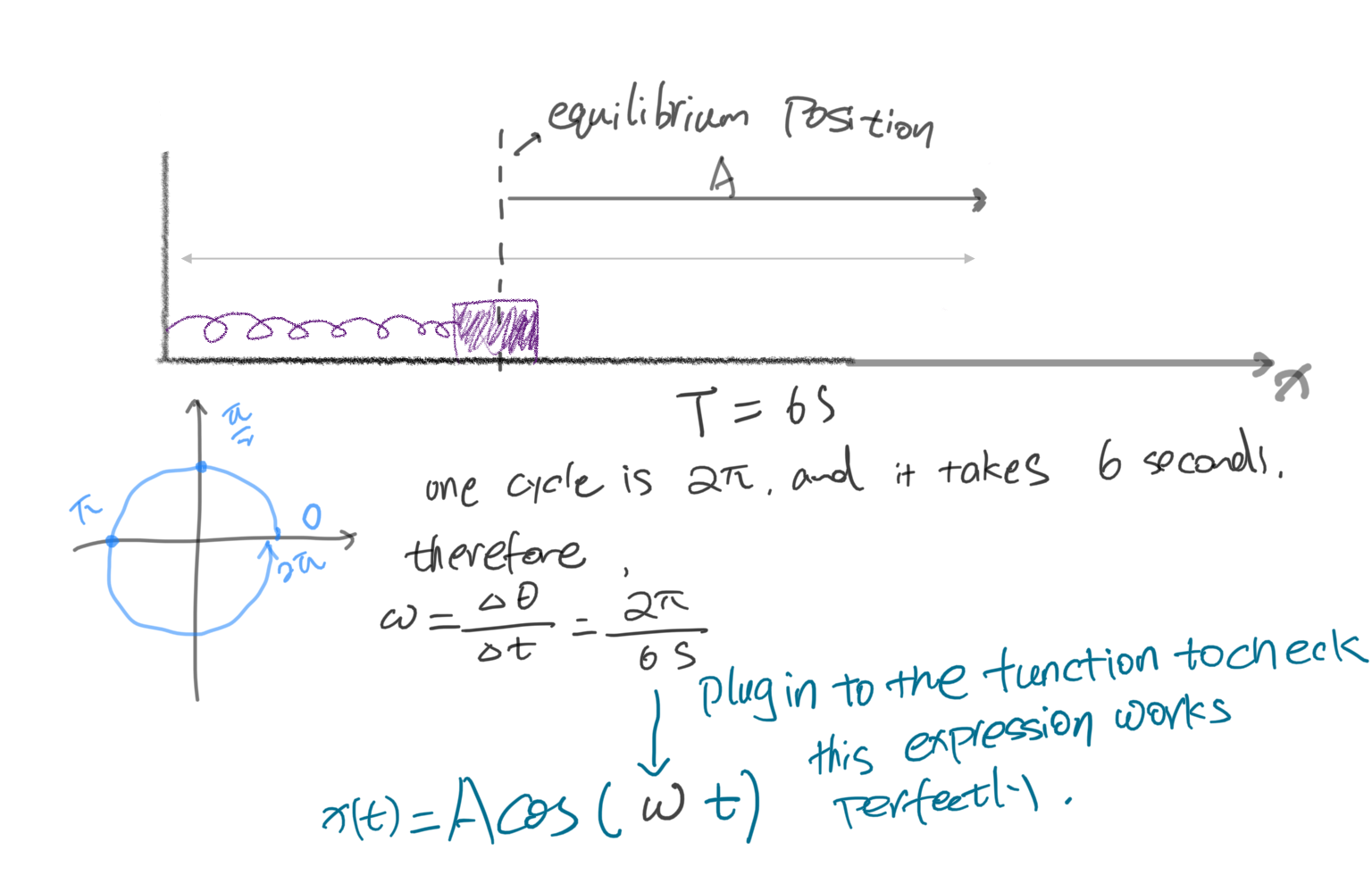
余弦的周期就是 $2\pi$,但我们的曲线周期未必刚好是它,而且,时间的表达通常是分、秒,而非弧度。于是这个表达式 $A\cos(t)$ 仍没有完善。假设现在的振荡系统周期是6秒,应如何在函数中表达?
现在引入一个重要概念——角速度/角频率 angular velocity / angular frequency $\omega $ . 它表达了单位时间内的角度变化,或者说旋转的速度。$\omega=\delta \theta / \delta t $(角度的变化量除以这一变化过程所经历的时间)。
c. 旋转速度乘上经过的时间便能得到实际的角度,这就很好理解了,现在函数就进一步完善为 $A\cos(\omega t)$
D. Phase 相位
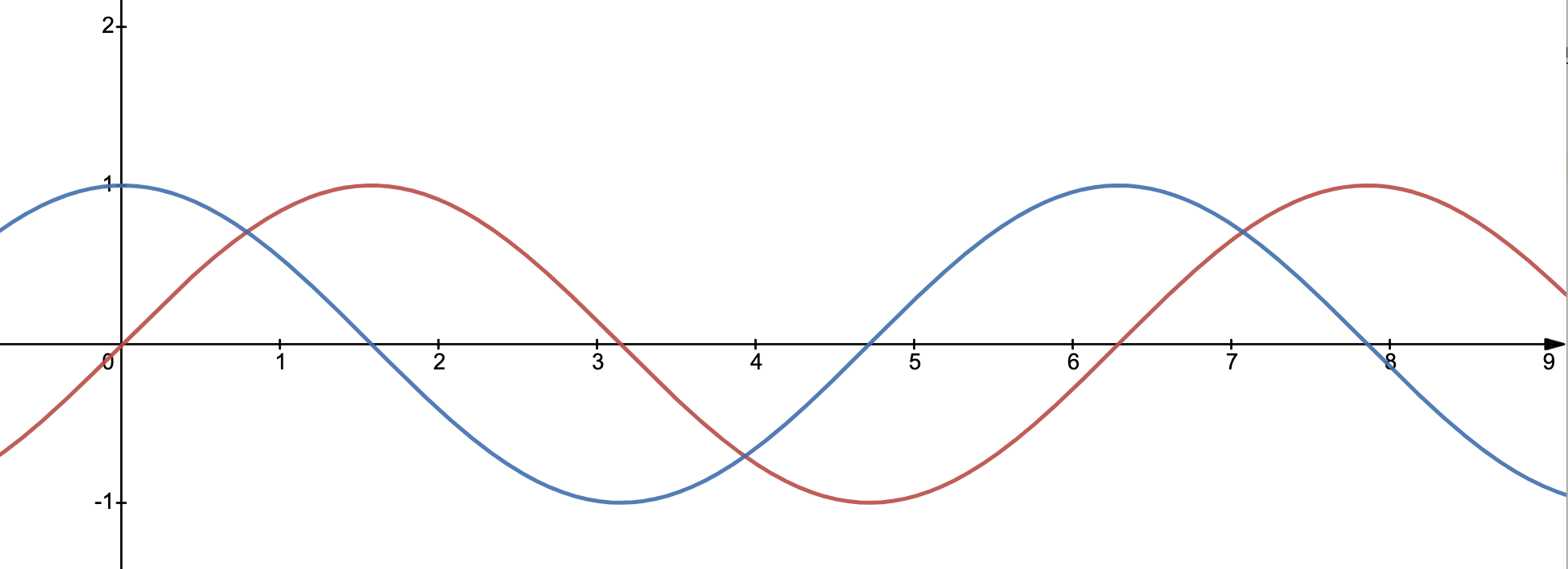
回忆小时候的数学课,正弦曲线从y=0开始,如上图红线。余弦曲线从y=1开始,如上图蓝线。思考:这两条曲线是否等同?
显然,它们是不同的两条线,否则它们应该重叠到一起。但是它俩的确拥有完全一致的周期和振幅。如果把红线向左移动 $\pi/2$ 的距离(或者余弦曲线往右走 $\pi/2$ ),两条线就会完全重叠。
还可以这么想:原本只是一个曲线,我们拷贝了一个副本出来,这个副本被平移了一些,于是得到另一条线,这个平移形成的差距,便是所谓的相位。上图两条曲线,可以说,具有“ $\pi /2$ 的相位差“。
两条原本具有相同属性的曲线具有一定的相位差,这样的状况可以描述为 out of phase ,可以翻译成“异相” (注意有些地方将异相按照狭义理解,表示“反相”,这里,我使用异相作为一个更泛泛的含义,即“不同相”的情况都是“异相”) 。如上图,可以描述为 one quarter of a cycle out of phase ,异相四分之一周期。
【注】我们现有的很多数学表达都来自对英文的翻译,在语意上难免发生不准确、有歧义的情况。有些差别微妙的不同词,在中文里甚至可能会使用同一个词来表达,请尽量以英文为准。
那么如何在数学上对phase进行表达?
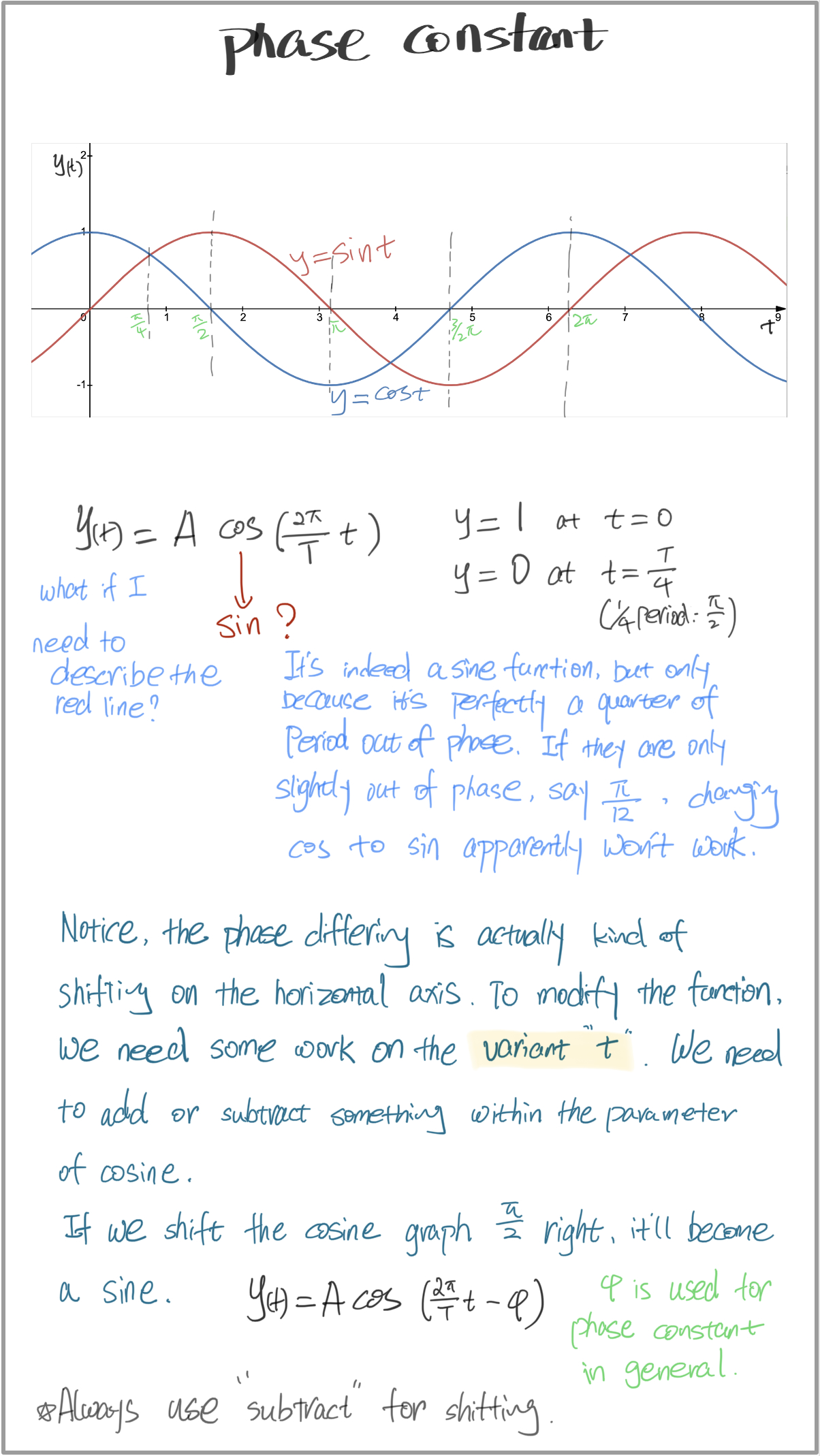
这样我们才终于得到完整的正弦型函数的表达式。
$$ y(t)=A\cos (\omega t-\phi), \ \ \omega=2\pi /T $$
作为惯例,一般使用余弦而非正弦作为sinusoidal function 的表达,可能是因为余弦起始点为1,正弦是0,在很多工程领域,可能需要起始点不为零。
E. 阻尼振荡
完美的周期运动是在理想条件下实现的,即没有任何阻力和能量的损耗,现实里,一个振动体
如果没有任何支撑其持续运动的力量,它总会不断减小振幅直至振动停止。这样的振动状态称为 damped oscillation 阻尼振荡,或damped vibration 阻尼振动。
大部分声学乐器,按下一个键盘或者拨动一根琴弦,它所形成的振动会在一定的规律下不断衰减。
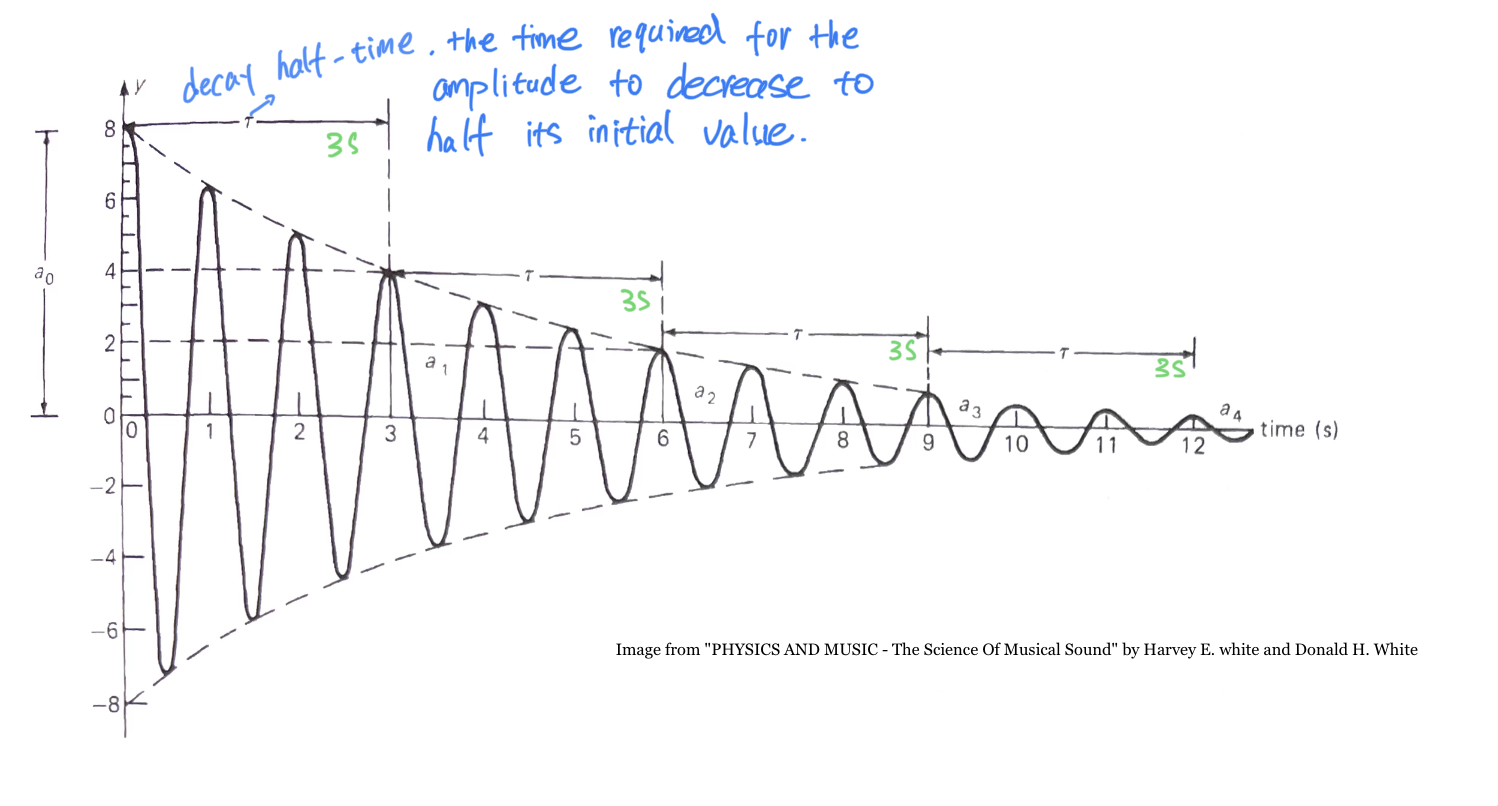
阻尼振荡的衰减呈现一个有趣的特征,即“半衰时间”,用希腊字母 $\tau$(tau) 来表示,指的是振幅下降一半所需要的时间,而这个时间独立于振幅值,并且在整个时间轴上形成有规律的周期。比如上图,振幅从8降到4经过了三秒的时间,从4到2也是三秒,从2到1又是三秒,可以写作 $\tau=3$ .
[========]
无论是宏观世界还是微观世界,波普遍存在于每个角落。波的种类也非常多,大体都能够归类为两种:横波与纵波。横波的介质振动的方向与传播方向垂直;纵波的介质振动与波的传播平行。
【disturbance - 波的本质可以理解为一种“扰动”】
当一个系统或介质受到外部力量或能量引起的扰动时,这个扰动会以波的形式传播。
波通常由两个关键要素组成:扰动和传播介质。扰动是导致波产生的原因,它可以是物体的振动、声音的产生、电磁场的变化等。传播介质是波传播的媒介,可以是固体、液体、气体或真空。
当扰动作用于介质或系统时,它会引起局部区域的能量或物质状态发生变化。该区域中的粒子或物质受到相邻粒子的影响,并将能量或信息传递给相邻区域,从而使波从源头向周围传播。
在传播过程中,波会以特定的频率和振幅在介质中传输能量和信息。不同类型的波(如机械波、电磁波、水波等)具有不同的特性和行为,但它们都可以被视为通过扰动在介质中传播的现象。
波可以被看作是由扰动引起的能量或信息在介质中传播的现象。
想象一根很长的绳子,绳子的一端在你手里控制,另一端稳固地挂在墙上。你手持绳子一端并上下晃动,这便给了绳子一个“扰动”,形成了“波”。
各种波中,横波是相对最简单的类型。横波的特征很容易在图像上表达出来:
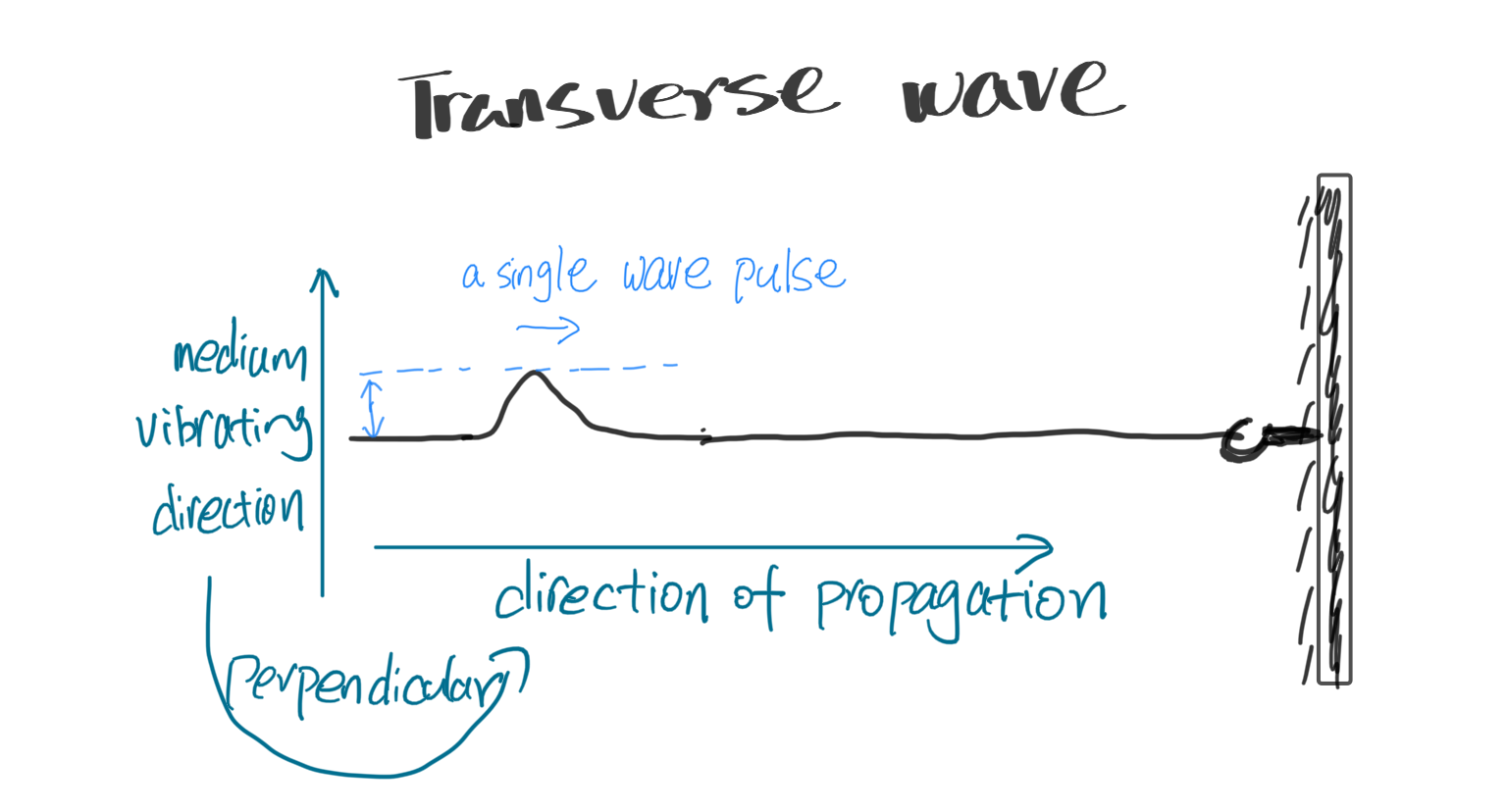
当你绷紧绳子,然后快速上下晃动一次,一个肉眼可见的“扰动”便会沿着绳子的方向传播出去,这样一个“扰动 disturbance”,有专门的说法,称为“横波脉冲 transverse wave pulse”。不要被这种很高级的词汇吓到,叫它"脉冲"不过是因为它是一个单独、孤立的扰动,而非连续的波。
[========]
正弦波
上一节讲到了简谐运动,如果拿着绳子的手也保持匀速的上下晃动,即进行简谐运动,绳子上就会形成一连串连续的波 ,即 “wave train”(这个表达是非常准确严谨的,但实际使用中常常省略为“wave”)。
这种由简谐运动引起的连续波动称为“正弦波 sinusoidal/sine wave”,这种波形叫做“正弦波/正弦曲线”。
所以,拿绳子的手由于“简谐运动”,给绳子带来一串均匀持续的“扰动”,由此形成了“正弦波”。请体会它们之间的联系。
$$ \text{SHM} \rightarrow \text{medium (with disturbance)} \rightarrow \text{sine wave} $$
[========]
声波
波的种类有很多,不夸张的说,波或许是整个物质世界的存在基础,声波仅仅是其中一种。微观世界里,分子、原子中的电子、质子、中子等以波动的形式在各自的区域内运动。在一定的刺激条件下,分子和原子还会发射出特殊的波,比如伽马射线、X射线、可见光波、微波等等。
宏观世界中的波动显然规模要大的多,甚至大到地震这种程度的超级振动,则是由地球板块的突然移动导致。水波由水体本身的运动以及风等因素造成,声波则是由空气中粒子的瞬间快速运动形成。
大体上,所有的波都可以分为横波、纵波两大类。横波是最简单、最易于理解和描画出来的一种,光波、弦乐器上琴弦的振动都属于横波。声音属于有些复杂的纵波。自然现象中的地震、水波往往是横波与纵波的组合。
横波 Transverse Wave
横波的形式比较好理解,而且一个简单的实验就可以呈现,那就是世界著名运动——“甩绳子”。
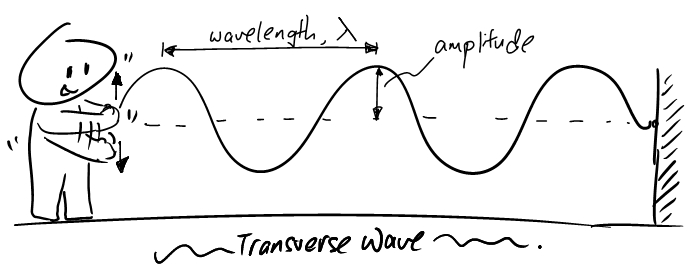
$\scriptsize\uparrow \text{image from www.socratic.org} $
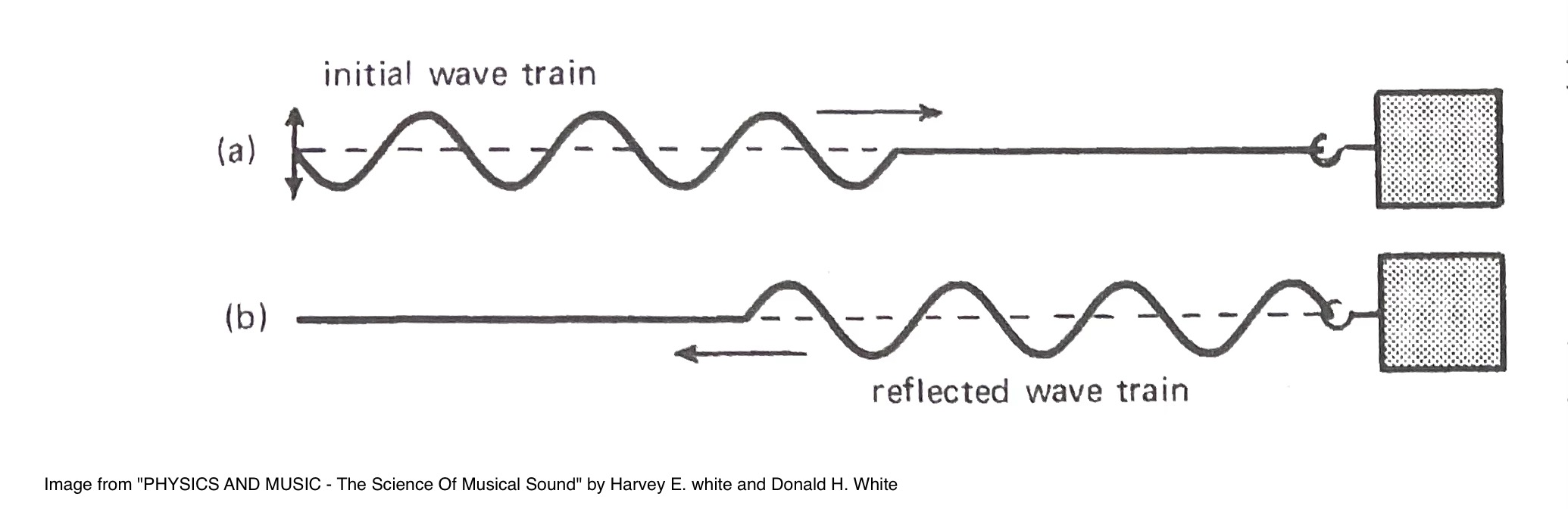
只要甩一下,就会形成一个单独的脉冲,这个脉冲会沿着绳子的方向一路走下去,如下图。这个小脉冲虽然是向上跳了一下,但它旅行的路径方向却是沿着绳子向前 —— 振动方向与传播方向垂直这便是定义了一个波为“横波”的根本特征。

如果你不只甩一下,而是持续做简谐运动,就会在绳子上形成一个周期波,它的传播方向是横向的,但你可以看到振动体本身是纵向上下的。把这个波用图像呈现出来就是我们最熟悉的正弦波了。
周期波基本属性 properties of periodic wave
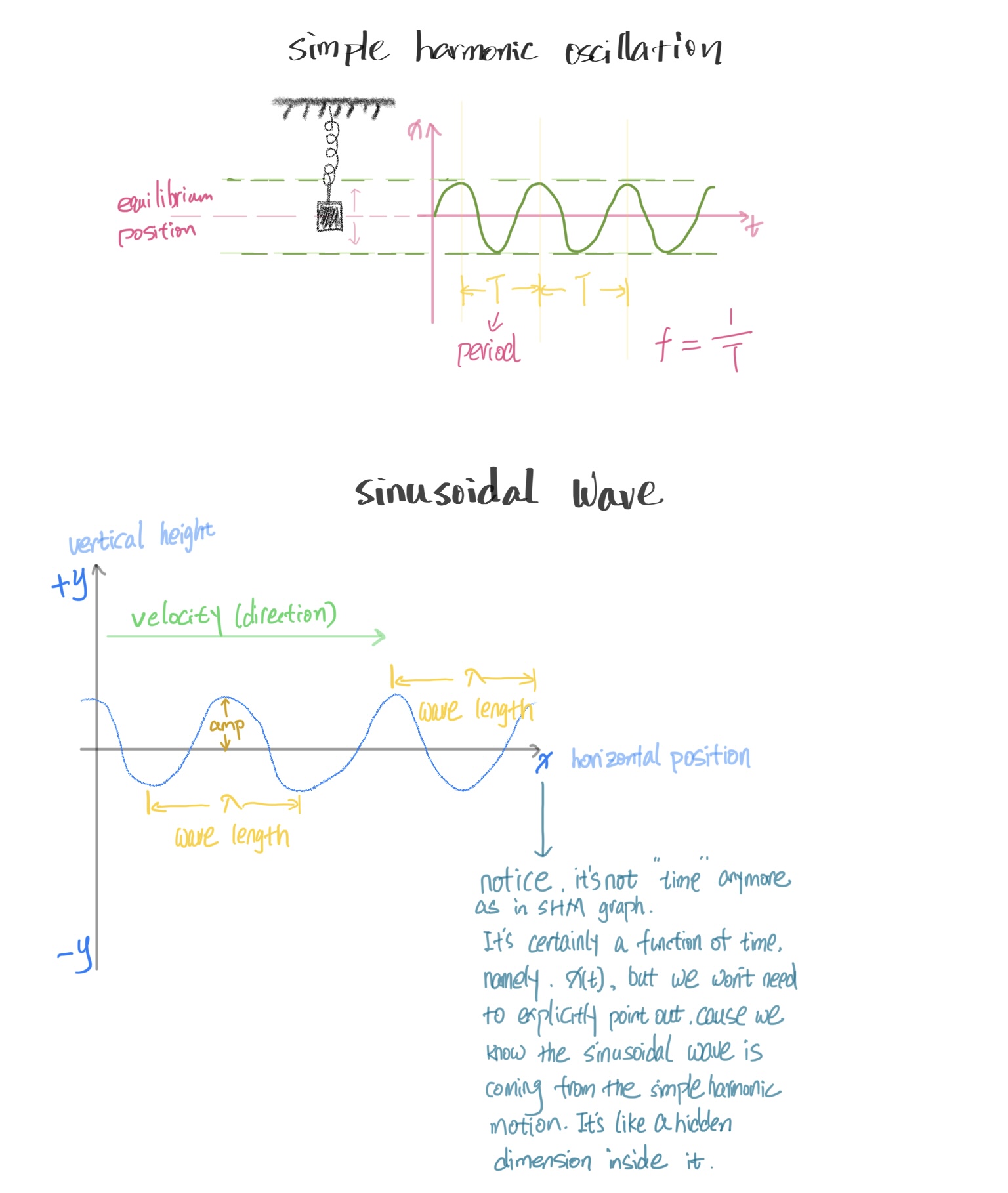
-
正弦曲线中,最高值称为波峰(peak),最低值称为波谷(trough)。
振幅(amplitude) 指从中心位置(即横轴)到波峰的这段高度。
如果你看到“wave height”这个词,有的时候它可能等同于振幅,但在某些语境下,它有可能指代波峰与波谷之间的距离,也就是振幅的2倍。 -
正弦波周期性地抵达波峰和波谷,是一个运动过程。
$\heartsuit$ 思考:周期运动在多长时间里完成一个来回?默认时间单位为秒。
周期(period) 指的是完成一个来回所需的时间,在公式里常记作大写的T。假如这个波以3秒的时间走完一个来回,即 $ T=3\ \frac{seconds}{cycle} $ -
运动必然涉及速度的快慢。
$\heartsuit$ 思考:单位时间里(1秒)能走完多少个来回(完成多少个周期)?
频率(frequency) 指的是单位时间里(惯例为1秒)完成周期的次数,因此它是周期的倒数,记作 $f$,$f=1/T=\frac{1}{3}\ \frac{cycle}{second}=\frac{1}{3}\ \text{Hz}$,每秒钟完成 $\frac{1}{3}$ 个周期。频率有专门的单位:赫兹 Hertz,简写为Hz 。 -
简谐运动造成了波的形成,这个波在宏观上一直移动,于是涉及到了距离相关的概念。
$\heartsuit$ 思考:这个波一个周期内走了多远?
波长(wave length) 一个周期里波走了多远,即波长 $\lambda$ 。在图像上可以以任意一点作为起点,到相邻的下一个等同点之间的距离便是波长 (注意,等同的点必须是位置、方向均一致的点,即“完全重置”的点) -
波在移动、行进,必然有速度的考量。
$\heartsuit$ 思考:如何表示波走的有多快?
波速(velocity) 波的传播速度,即单位时间内波行进的距离。我们都知道速度=距离/时间,这里的距离指的正是波长,完成一个波长的时间当然就是周期,因此 $\text{velocity = wave length/period}, v=\lambda / T=\lambda f $ 。从这一等式中看到,提高波长或者频率都会让波速增大,这是符合直觉的。
example
仍然是甩绳子的场景,绳子一端固定,另一端以12.0 Hz的频率上下运动,波以15m/s的速度向另一端行进。计算出波长。
$v=\lambda f \ \Rightarrow \ \lambda=\Large \frac{v}{f}$,因此,波长 $=\frac{15m/s}{12 c/s}=1.25m/c$,波长是1.25米。
[========]
纵波 Longitude Wave
声音是怎样传播的?
当你拨动一根琴弦,使得这根弦以及整个乐器产生了周期振动,这些振动压向它们周围的空气,一团空气粒子被推动、压缩,这股能量紧接着传递到这团粒子旁边的另一团粒子,就这样一个接一个,空气中产生了周期性的扰动。
与绳子的起起伏伏不同,空气中的粒子被推拉进而运动的方向,即媒介的振动方向与整个波的传播方向平行,这正是纵波的特点。
为了把空气粒子被推拉的过程形象化,仍然可以用到弹簧。这次,一段很长的弹簧水平展开,右端固定,在左侧这一端,给弹簧一个向右的推力,这将形成一个 “纵波脉冲” longitude wave pulse 。这个脉冲匀速抵达另一端,之后反弹回来。
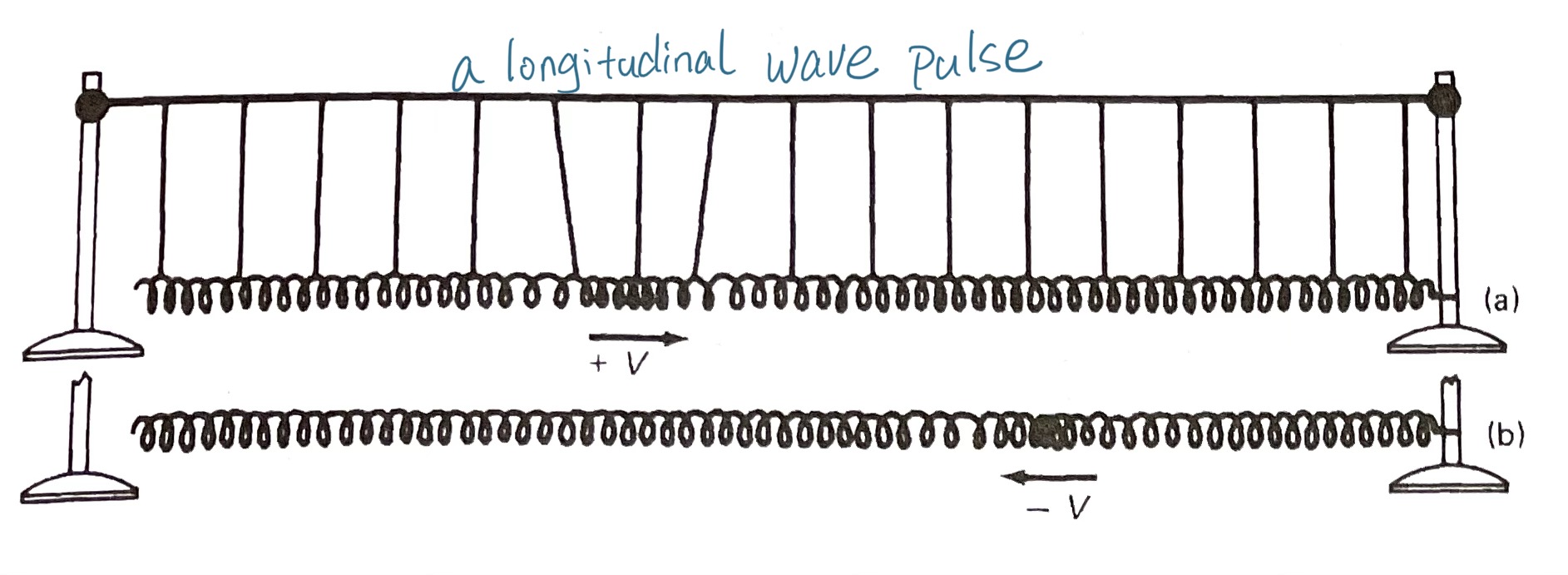
如果在左侧以简谐运动的状态持续推拉弹簧,这将形成连续的纵波。可以看到弹簧有的地方密度集中,形成了 “密部/压缩区” compression,其他较松散的地方便形成了 “疏部/稀疏区”rarefaction 。
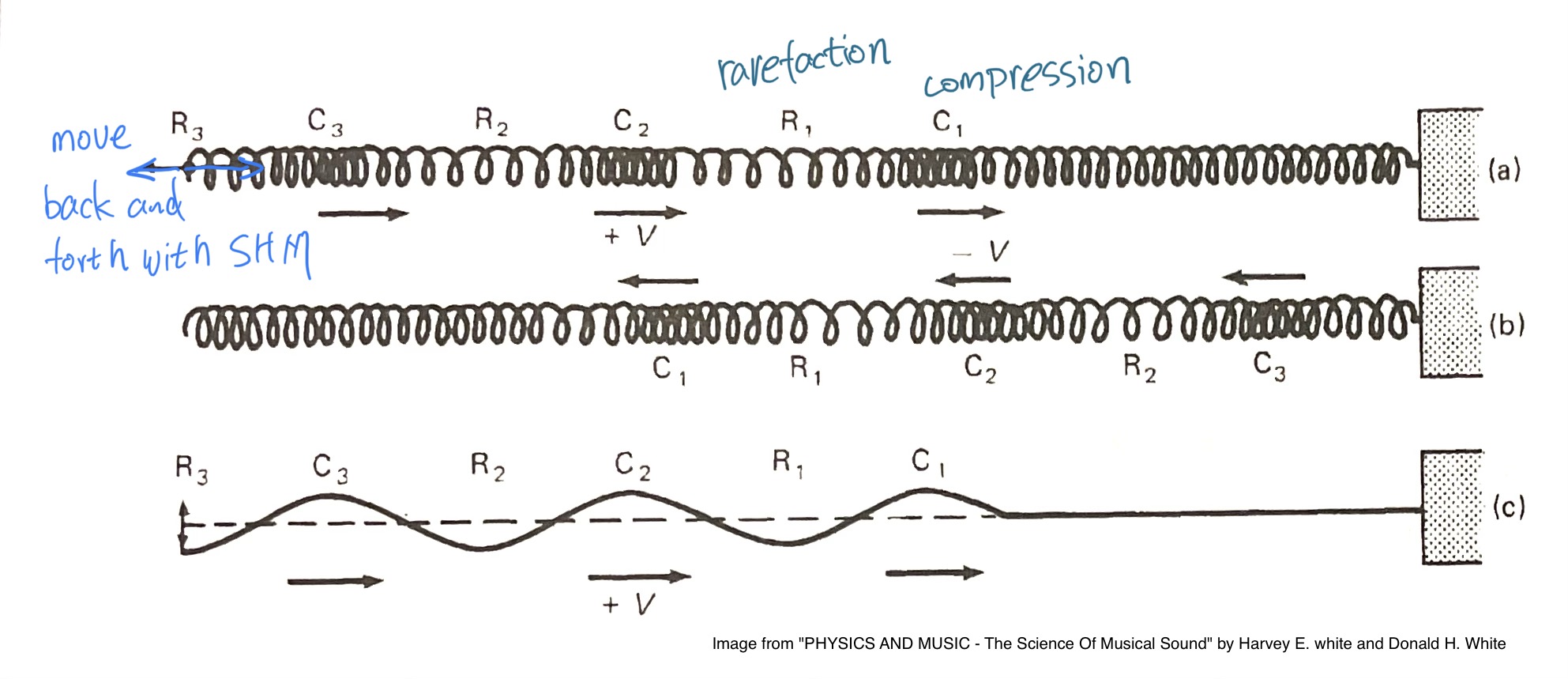
波在媒质中传播的过程可以用高尔夫球-弹簧模型以逐个扰动分解的方式演示出来:
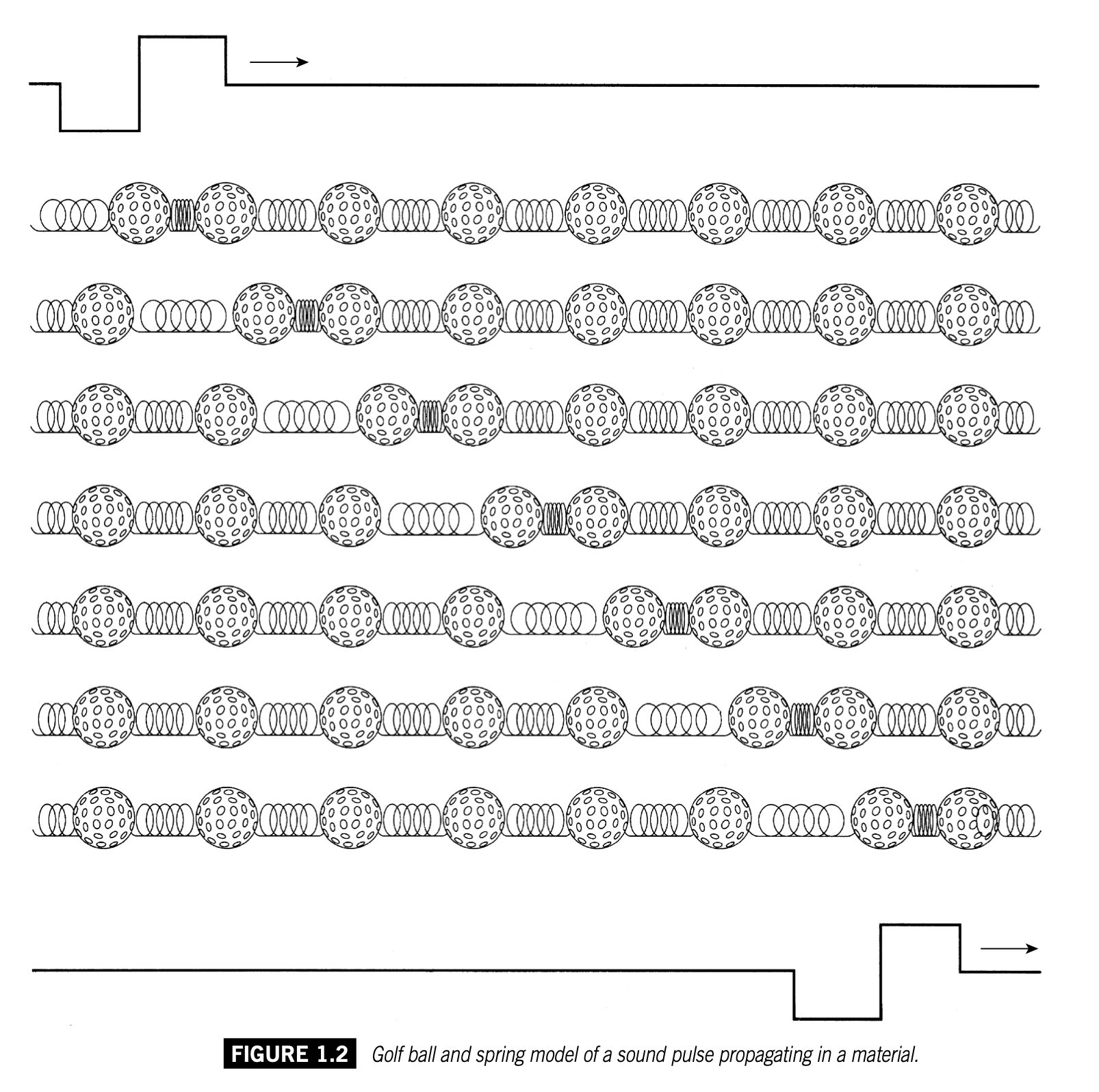
高尔夫球本身就是媒质。在真实场景中,如声音通过空气传播,空气中的粒子总是要回到平衡位置,扰动的过程就是“压缩-稀疏-压缩...”不断反复的过程。
纵波很难用函数曲线清晰表达,正弦曲线只能相对的模拟波的变化和周期特征。其中波峰的部分代表密部,波谷代表疏部。
[========]
声波的传递
- 为什么真空中没有声音呢?
所谓声波,必是有某种媒介(主要是空气)产生振动,才能形成波。空气的振动传递到人耳中,刺激了鼓膜的振动,才有可能让人脑“解析”出声音。没有任何物质的真空里,没有形成振动的实体,就无法产生波,声音也就无法传递了。
声音在气体、液体、固体中都能够传播,在不同的环境下,传播速度不同。液体和固体中的声速远大于空气中的速度,空气中:331m/s; 水中:1435m/s;钢铁中:5130m/s; 钻石中:14000m/s。
- 反射 折射 漫射 衍射
声波也会产生类似光波的反射、折射等现象,这里先记录一个最能体现声波在不同情况下的介质中传播特点的折射现象。
-
- Refraction of sound waves
折射是当波传播介质发生变化时,波速变化从而导致波传播方向发生偏转的现象。
假设你在一个不大的湖边露营,白天你看到湖对面有其他的队员,但是听不到他们说什么。然而到了晚上,你不仅看得到他们,还能听到他们说话的声音。
空气在不同的高度,温度不同。声波在温度较高的空气中传播速度更快。通常,高度越高,空气温度越低。当靠近地面的声波向远处传播时,最低处的那部分传播最快,越往高处,声波速度越慢。这会导致声波路径发生偏转,相当一部分声波向上弯曲,甚至可能扩散掉,于是未能传播到更远的地方。所以白天你没能听到湖对岸的声音。
但是在夜晚,会出现逆温现象 (temperature inversion),靠近湖面的温度相对更低,上方空气温度更高,声音的传播速度也随着高度增加而增大。离湖面高度最远的那部分声波传播速度最快,靠近湖面的区域传播更慢,声波的方向朝下弯曲,进而抵达了湖对岸使你听到他们的声响。当然,对面的人们也同样听得到你说话的声音。
这种现象主要发生在日落后,地面温度迅速降低、高空温度仍然较高的时候。有些声学专家和历史学家发现,声音的折射现象曾经甚至很大程度影响了某些历史战争。
- 共振/共鸣 resonance
我认为,共鸣现象的存在进一步直观证明了声音的本质是振动能量的传导过程。
共鸣的定义很好理解,两个固有频率相同的发声体,拉开一点距离放置,给其中一个振动激励使其发声、另一个不操作,一小段时间后,你会听到原本静止的那个发声体也以同样的频率振动起来并发出了声音。
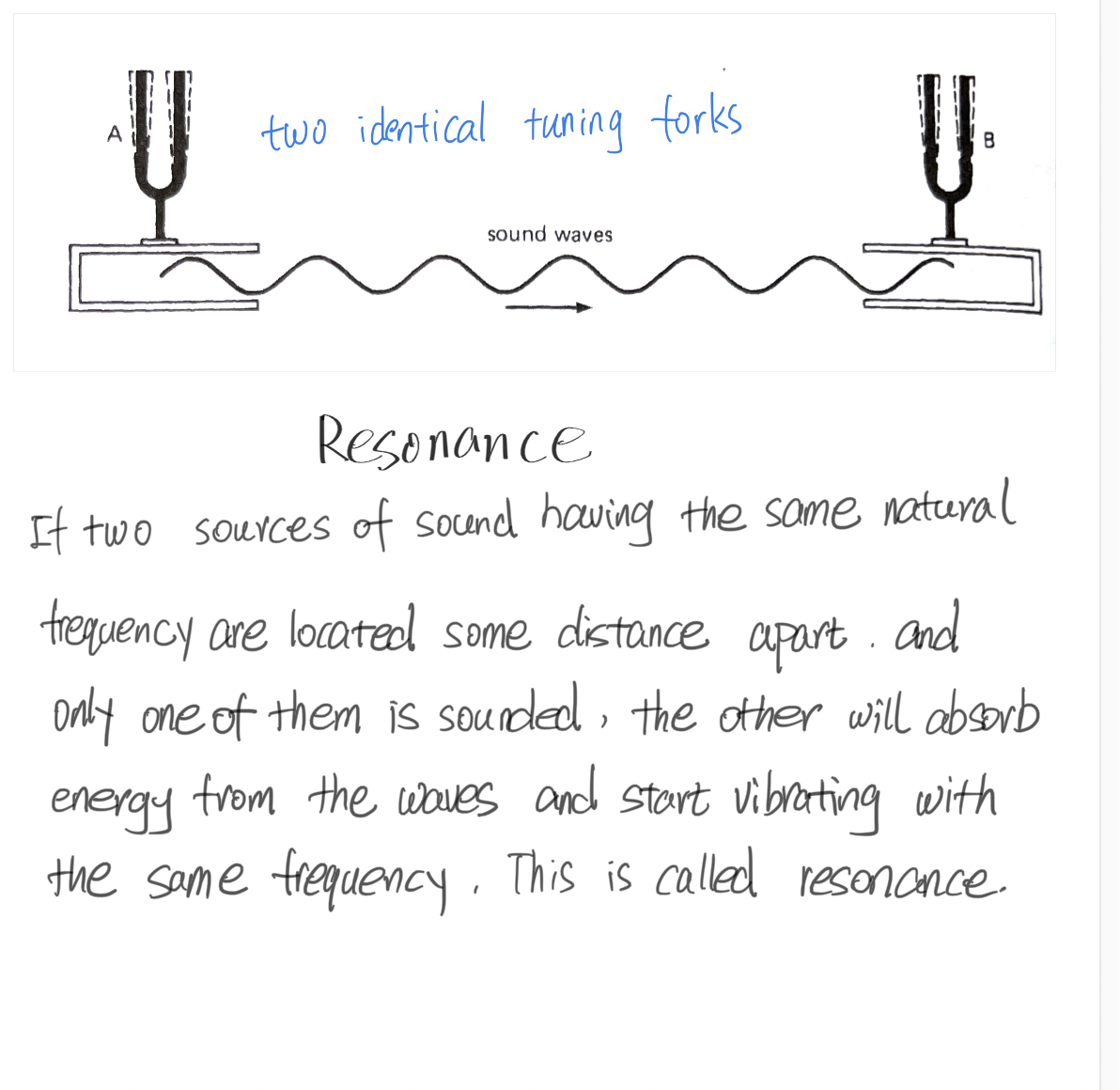
共鸣这个词,在很多语境里都不等同于物理现象中的“共振”。音乐家们已经习惯了用共鸣 resonance 这个词来表达室内声音反射的现象。比如一位歌唱家或许会说:这个教堂的共鸣特别好。实际上,他所指的现象,用准确的物理名词来说,应该是混响 reverberant 。共鸣声本质上就是“共振”这种物理现象,只是在声音领域,人们更习惯说“共鸣”。
如果两把调音完全一致的小提琴放置在一起,拉响其中一个的琴弦,会听到另一个同频率的琴弦也随之振动了。
- 多普勒效应 The Doppler effect
多普勒效应是几乎每个人都曾体会过的,在初高中教材中也曾出现过。飞驰而过的救护车是最典型的例子。这种声音效应的重要特点是:音调变化快速且连续。
从远处而来的声源靠近听者之后再次远离,声音听起来经过了升高又下降的过程。产生多普勒效应的关键在于声源和听者之间的相对运动。
如果一个静止的汽车发出汽笛声,周围同样待在原地的听者无论站的多远,大家接收到的都是真实的频率,声波不会在任何方位累积。声波是全方向传播的,听者无论位于声源的哪一侧,大家听到的都是一样的音高。
当汽车鸣笛时是移动状态,如上图所示,车朝左开去,在车的周边不同方位都有听者。汽笛的声波朝所有方向发出去,但是汽车驶向了左侧。由于汽车一直朝左开,每一个新发出的波紧随在已经传播出去的波之后,并且离前面的波越来越近,波的密度不断增加,声波波长变短,位于这一方向的听者耳朵接收到了比真实声音频率更高的振动频率,于是听起来音调变高了。与此同时,车在不断远离车尾的方向,向车后方传播的每一个波,逐渐拉开了距离,波的密度降低,声波波长变长,导致人听到了音调更低的声音。但在车的两侧与其大致成直角位置上的听者,声音听起来没有明显变化,因为声源没有相对靠近或相对远离。
有些声音我们听起来是悦耳、清晰、明确的,有些声音是杂乱无章的。所有声音可以简单划分为两大类,乐音和噪音。噪音暂且不纳入当下的学习范围里,现阶段说到一个“声音”,基本上默认是有明确音高的简单声音。
声音有无数种可能,如果要描述一个声音自身的基本特征,有几个不得不说的“参数”:
| 强度-响度 | 频率-音高 | 波形-音色 |
|---|---|---|
| intensity-loudness | frequency-pitch | waveform-timbre |
如果我们面对的是简单纯音,只需要谈论它的振幅和频率即可,这两样最基本的特征决定了一个声音的身份。而对于复杂音,尤其是乐音,则有更多复杂的属性决定了某声音的特征。
一个声音听起来是“什么样”,既取决于它自身的物理特性,也取决于我们自己的听觉系统和神经系统对它的反应。这些具体的物理性质和相互之间的关系是我们要关注的。
Part II 从物理振动到听见声音
声音是有能量的,这一点已经有无数物理实验证明过。强度是声音基本特征之一,对声音能量与强度的测定体现在声强级、声压级、声功率等诸多物理标准中。强度 intensity 指的是物理特性,与之相对,人对此的主观体会称为响度 loudness,人感觉到的“有多响”与声音自身的物理强度往往是不一致的,这正是由于人类特别的听觉系统。
声强与声压
声音领域的名词和单位似乎很多很复杂,如声强、声压属于绝对量值,但在实际使用场景中常用声强级、声压级这个以分贝为单位的相对量级。
声功率与声强 Power and sound intensity
首先解释声功率。无论声、光、热、电等等,对于能量(energy) 的测量都用焦耳(joules, J)为单位。功率(power) 指的是能量转换/能量流动的速率,单位为瓦特(watt, W)。 $ 1\ \text{watt}=\frac{1\ \text{joule}}{1\ \text{second}} $
声强被定义为单位面积上的声功率(度量声波在某个方向传播的功率密度):
$\text{Intensity}=\Large\frac{\text{power}}{\text{area}}$ $(W/m^2) $
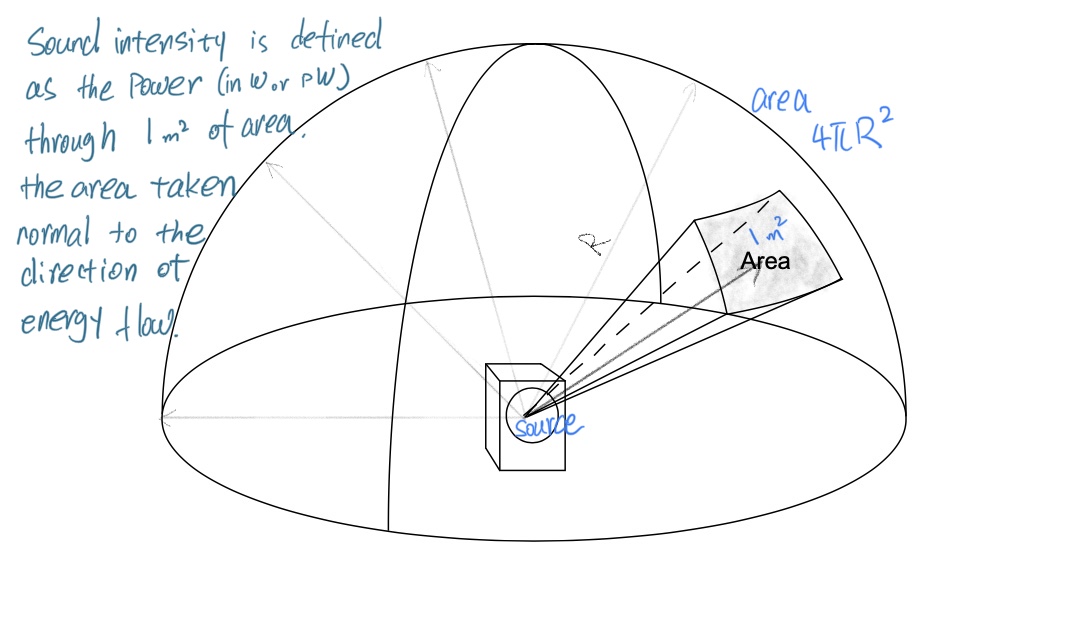
但对于现实生活中常见声音的强度测量,瓦特这个单位显得太大了,尽管有能量,但我们日常听到的那些声音强度很小,因此在实际使用中用到一个小单位皮瓦(picowatt, pW),$ 1\ \text{pW}=10^{-12}\ \text{W} $,这个相当微小的数字是非常有意义的,它是我们人类能够听到的最轻微的声响,如此微弱的能量都可以被我们的耳朵捕捉到,足见人类听觉之厉害。
声强的符号常用 $I$ 来表示,1皮瓦这个常数因其有特殊意义,被赋予了常用符号 $I_0$ ,(也可以写作$I_{ref}$ ,即参考值之意) (注意它不表示变量,而是特指这个常数),后面会用到。
[========]
平方反比定律 The inverse squre law
声音为何变弱?
了解声强的概念后,就可以知道离声源距离越远、声音听起来越弱这一现象的物理原理并计算不同距离下声强的变化了。
理论上,声波只要没有阻力,就可以永恒沿直线传播下去。但即使在空旷的户外,声音显然也会随着距离拉远而明显减弱。利用声波的传播特点和声强公式可以解释这一点。
声音的传播是全方向的,一个点声源理想上可以朝着整个空间的所有方向辐射声波,这使得振动面成了一个球面,声音占据了一个立体空间,有时声波会被描述为是一种“球面波”,指的就是这种辐射传播的特性。
一个著名的问题:听者与声源之间的距离翻倍,声强会怎样变化?
直觉猜测或许是减半?
从计算上可以看出来,不管声源本身的功率是多少,不同距离位置的声强比值总会受到 $r^2$ 的限制,最终我们得出来了平方反比定律 这项重要规律。
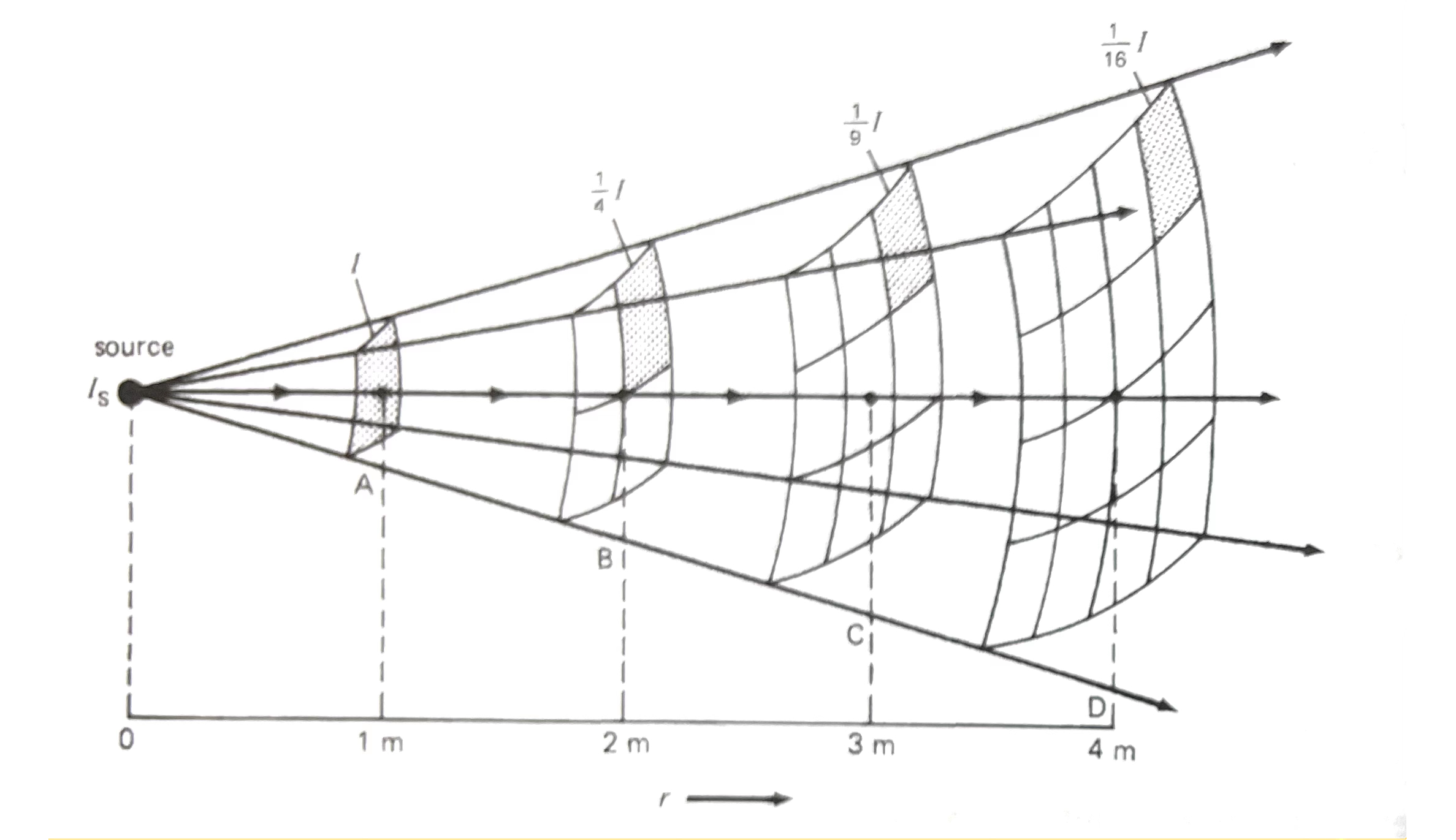
这个数学关系可以简单表达为:
$$\frac{I_2}{I_1}=\frac{R_1 ^{\ 2}}{R_2 ^{\ 2}} $$
[========]
声强级 Sound Intensity Level
现实生活里从没见过用瓦特数来表示声响的大小,声强的绝对测量值数字太复杂了,而且人类对声音强度的感知范围相当宽广($1~10^{12} pW$),1皮瓦代表了听阈 threshold of hearing,1瓦特(即$10^{12}$ 皮瓦)代表了人类听觉能承受的极限——痛阈 threshold of pain。
如此复杂而大范围的数字系统显然不适合普及使用。人们采用了一种对数型的强度量表(之所以用对数,正是基于Weber-Fechner定律的发现),这种量度称为声强级,可简写为SIL,分贝作为单位。
韦伯-费希纳定律(Weber-Fechner Law)是心理物理学中的一个重要原则,用于描述感知刺激强度和感知体验之间的关系。感知到的刺激强度与实际刺激强度之间的关系不是线性的,而是对数关系。
分贝(Decibel,缩写为dB)是一个用于度量声音强度、电压、功率和其他物理量的单位,是基于对数比例的单位,常用于描述相对值。在声学中,分贝用来表示相对于参考强度的声音级别。
分贝,即十分之一“贝尔”。贝尔 Bel 是一个重要的数学单位,以电话发明者贝尔命名。在声学领域,由于声音能量很微弱,贝尔作为单位也显得太大了,不易于记写,于是使用它的十分之一作为一种单位,这便是decibel,这个词的本意就是“十分之一贝尔”,这就是为什么分贝记作dB。
注意到分贝这个单位的关键含义在于“与参考值的比例的对数。如果要计算声强级,必须首先明确“参考声强”是什么,不然就没有测量的意义了。
声强级的计算正是以我们的听阈—— $ 10^{-12} W/m^2 $ 作为参考标准。根据贝尔的定义,1贝尔的声强级为某个声音的声强与参考声强比值的对数。1贝尔等于10分贝,所以选用分贝作为单位时,要将物理量的值乘以10。由此,我们得到声强级的计算公式:
$$ \text{SIL}=10\log_{10} \frac{I}{I_0} $$
现在,回过头来去看前面已经得知的一些数据,把它们全部转换为SIL后,看起来就清晰简单的多了。
人的听阈代入公式后得到0dB,当然听阈值本就是分贝计算中的参考值,所以它就是整个量表的零点。(注意这里的“0dB声强级”不同于数字音频设备上的0dB,为了区分,将保留“声强级”或SIL作为单位的一部分),人的痛阈值 $10^{12}$ 意味着 120dB SIL .
根据定义,我们可以计算出相对强度以及其对应的SIL,并总结出表格,在这份数据中,你可能会发现一些重要的规律。
| relative I ($I/I_0$) | SIL, in dB |
|---|---|
| 1.00 | 0 |
| 1.26 | 1 |
| 1.58 | 2 |
| 2.00 | 3 |
| 2.51 | 4 |
| 3.16 | 5 |
| 3.98 | 6 |
| 5.01 | 7 |
| 6.31 | 8 |
| 7.94 | 9 |
| 10.00 | 10 |
当强度翻倍时,SIL增加3dB。
再次回顾平方反比定律,当听者距离翻倍时,比如从1m走到2m处,声音强度变为原来的1/4,转换成分贝:
$$ 10\log_{10}\frac{1}{4}\approx -6 dB $$
_从2m走到4m,强度同样变化到2m处的1/4。那么相比1m处,强度为1/16,在前面的基础上应该再减去6dB。将1/16代入分贝计算的式子里,确实得到了-12dB。由此可知,距离翻倍,声响会降低6dB SIL。
[========]
声压与声压级 Sound pressure and SPL
声学工程领域常见一种设备——声级计 Sound level meter,是用来测量声压的工具。

与“声强”不同,“声压”是另一种测量声音强度的标准。声强可以描述声波在某一点的幅度大小,理论上很有用,但声压是更为常用的描述声波大小的物理量,而且声压更易于测量。不过,先理解声强的概念是非常有必要的,并且二者之间也有数学关联。
声压的定义,简单来说就是单位面积上的压力,压强单位 $Pa=N/m^2$ . 回忆作为“纵波”类型的声波,它的波动形式体现在空气粒子有规律的反复压缩、稀疏,由此形成周期性呈现的“密部”与“疏部”。所以声波也是一种“压力波”,压力周期性变化,类似简谐运动,于是可以用正弦曲线表达出来。
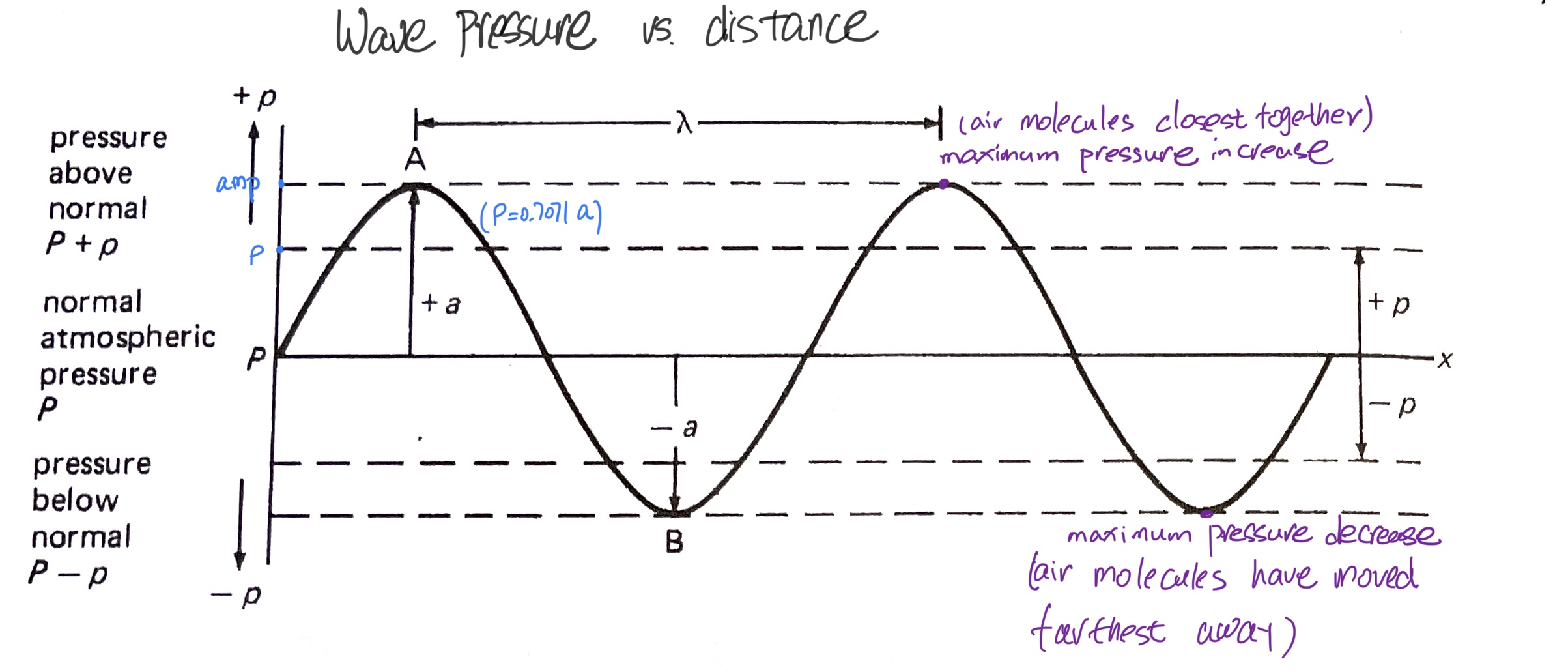
空气压力的变化以一个“平衡点”为中心,上下来回,这个平衡位置就是标准大气压,即空气粒子没有受到压力刺激时的静止状态 。回忆声波的模拟实验,每一个粒子在它的平衡位置两侧来回(而非跑到别的地方去),并推动边上的其他粒子运动(能量的传导)。
图上可以看到,声压与振幅同步变化,这很好理解,声音的幅度正来自于声波这种因压力变化带来的位移变化。声音的有效声压 effective pressure(p)是一个常量,即压强峰值(类似振幅)。声压与振幅之间有一个数学关系:$ p=a/\sqrt{2}=0.7071a$ 。
声强 $I$ 与 声压 $p$ 之间的数学关系:$ I=\frac{p^2}{Vd} N/m^2 $,V是声速,d是空气密度。
声音大小最重要的度量标准——声压级 SPL
与从声强到声强级的计算逻辑一致,从声压到声压级也是将绝对量度换算为以分贝为单位的比率的计算过程。计算SPL用到的参考值是 $20 \mu Pa\ (20*10^{-6}Pa)$ ,记作 $p_0$。
回忆声强的参考值是人的听阈,20微帕这个极弱的压强对应的其实是同样的听觉极限(1kHz听阈),在参考声强 $I_0$ 条件下,声压约为20微帕。而声压的上限——痛阈值为20帕。
$$ SPL=20\log_{10} \frac{p}{p_0} $$
我们已经知道“贝尔”这个单位的数学意义就是“与参考值的比例取常用对数”,由于要使用小单位“分贝”,所以计算上再乘上10,但是SPL的计算却是乘了20。这样在计算上使得SPL基本可以用整数来表达(因为要除以20)。另一个重要因素在于,这个换算方式将SPL与SIL紧密联系起来。
利用声强 $I$ 与 声压 $p$ 的换算公式来计算SIL ($Z=Vd$ ,代表声阻抗率,用$\lg \text{代替} \log_{10}$,以简化表达式):
$$ \text{SIL}=10\lg \frac{I}{I_0}=10\lg \frac{\frac{p^2}{Z}}{I_0}=10\lg \frac{p^2}{ZI_0} $$
可见,声强与声压的平方成正比。将对数中的平方提到系数去:
$$ \text{SIL}=20\lg \frac{p}{\sqrt{ZI_0}} $$
这基本等同于声压级SPL的计算公式,只是参考声压换了一种写法,用这种方式来算$p_0$ 会发现数值是非常接近的。因此,SPL和SIL度量值大体等同,在单一声源条件下,二者基本等效。
当只有一列声波存在,(不存在反射声的情况下),声压级和声强级近似相等。比如10dB声强级变化将产生10dB声压级变化。
二者容易混淆,因此要事先弄清楚什么情况下使用哪个量。对于声音大小方面的问题,通常用声压级,声压比较容易测量,而且与听觉反应的关系最为密切。
[========]
对声响的感知
物理振动就是声音吗?
声音的各种可测量的物理属性与人的主观感知有一些特殊的联系,这属于心理声学的一部分。而感知的基础来自生理声学对听觉系统的研究。
我们都知道声音是一种波,声波来自真实的物理振动。但振动体本身并不是声音。人对声音的感知体验,不仅涵盖耳朵对振动的接收与传导、神经系统对听觉信号的解读,同时也包含了心理、情绪、文化背景等很多心智层面的解读。
从这一章节开始加入听觉系统的内容。
听觉系统
人耳的结构图和详细的工作原理在此略过,仅总结几项关键点。
外耳
- 外耳部分充当放大器的作用,同时也部分地作为滤波器来定位声音;
- 外耳道不仅连接内外耳,同时也是一个约2 kHz的共振腔,对语音放大起到作用;
- 鼓膜/耳鼓 eardrum —— 外耳与中耳的分界面,担当主传感器,把空气压强转换为中耳内的振动;
中耳
- 传输作用——三块听小骨(锤骨、砧骨、镫骨)负责把鼓膜的机械运动传输到耳蜗的淋巴液。
- 放大作用——听小骨能够通过杠杆作用进一步放大有效声压,这是为了耳蜗液体较高的阻抗(液体声阻抗大于空气声阻抗)。
- 保护作用——某些声响过大的情况下,保护听觉系统。
内耳
- 卵形窗oval window 连接中耳和内耳,机械振动从中耳镫骨底板通过卵形窗传输到耳蜗;
- 内耳关键组成部分是耳蜗cochlea,负责将机械振动转换为传输给大脑的神经电脉冲;
- 耳蜗内部是一个锥形腔且逐渐变细,不同频率会在不同位置上引起共振。
- 耳蜗内覆盖了一层小绒毛——基底膜 basialr membrane是内耳极为关键的结构,这些小绒毛将振动信号转换为神经信号;基底膜的宽度和厚度沿着耳蜗逐渐变化,不同频率的纯音信号将在基底膜的不同位置激发一个最大振幅。
[========]
响度感知
人耳的频响范围在20 Hz~20 kHz之间,不同人群的上限差别会很大,大多数成年人都达不到20 kHz的听力范围。自然声音大多数集中在中部区域(300~3000 Hz),但自然声音中的各次谐波会扩展到这个范围的极限甚至超过。即使是那些表观上很沉闷的声音中也可能包含微弱的高频成分。对频率的感知具体内容放在后面章节,本章节侧重声响。
等响曲线
声音的基本特征之一——强度,是对声音的客观度量,人耳对此的感知程度称之为“响度”,响度与声音本身的振幅大小相关,但也是主观的、且并不与客观声强简单对应。声音的强度可以用声强级或声压级表达,但响度却不能直接用这些物理量值。
人耳有着很宽广的频响,但对于不同频率声音的强度感知不同,或者说对不同频率的灵敏度不同。这其中的规律,前人们经过大量实验记录丰富的数据,并总结出了人耳的等响曲线 Equal loudness contours,这是一组曲线图,它也叫“弗莱彻-芒森 Fletche-Munson”曲线,弗莱彻和芒森是最早进行等响曲线测量的研究者。
这组曲线图中,每一条曲线代表一个响度,在这条覆盖所有可听频率的曲线上,基于不同频率的声音有着不同的声压级,但是,只要是一条曲线上的,它们的响度(人耳的感知)是一致的。
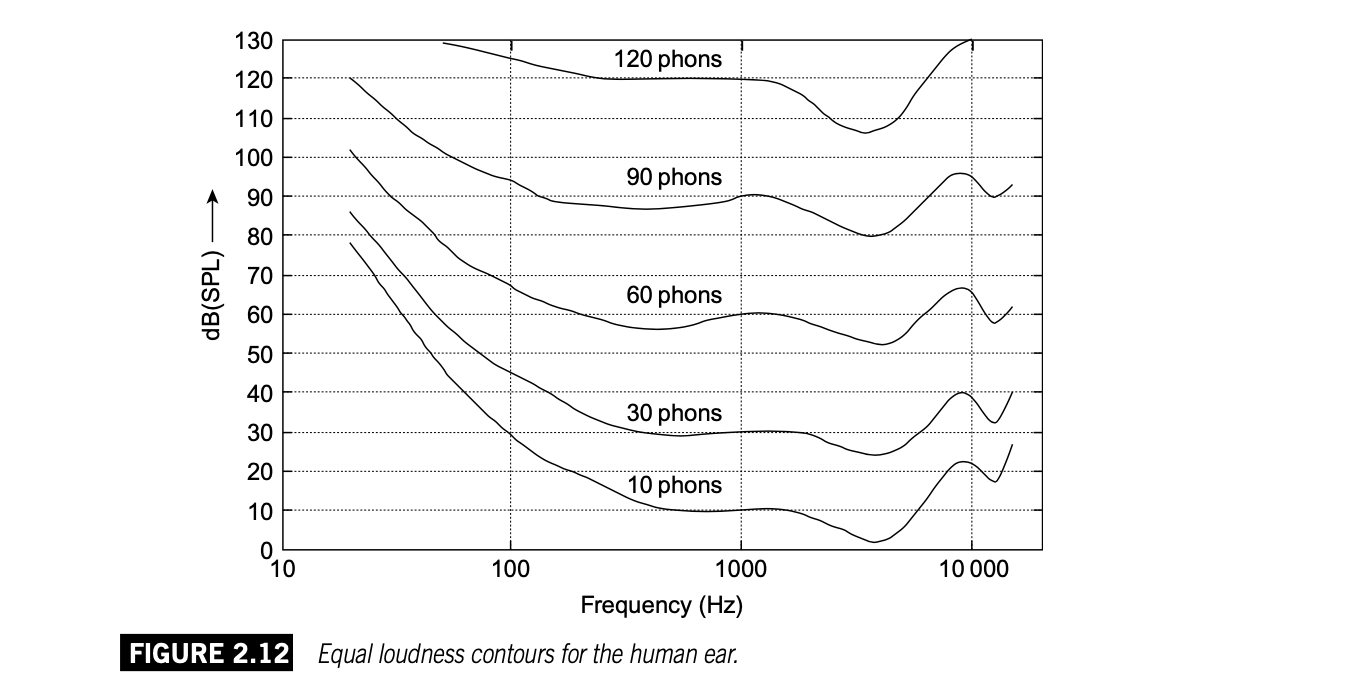
响度有它自己的单位,等响曲线中的方phon定义为:1方=1dB SPL的1 kHz纯音的响度。方并不是一般意义上的“单位”,它代表等响曲线图中的一条曲线,也可以说是一组数据。
“方”值是通过让听音者将声音与1kHz纯音的响度进行比较得到的。一个声音的响度级(方值)定位为和它同样响的1kHz纯音的声压级。注意1kHz是重要参考点,等响曲线中,N方曲线穿过1kHz的位置,对应的声压级就是NdB SPL 。
【注意】另一个响度单位宋sone (定义1 kHz的纯音在40dB SPL的响度作为1 宋,声压级每增大10dB SPL,响度(宋)变为原来的2倍),已经几乎不再被使用了,20世纪30年代,宋最初被用作响度单位,之后逐渐被方取代。现有标准下的等响曲线只有方。
一个更为完整的等响曲线图如下:
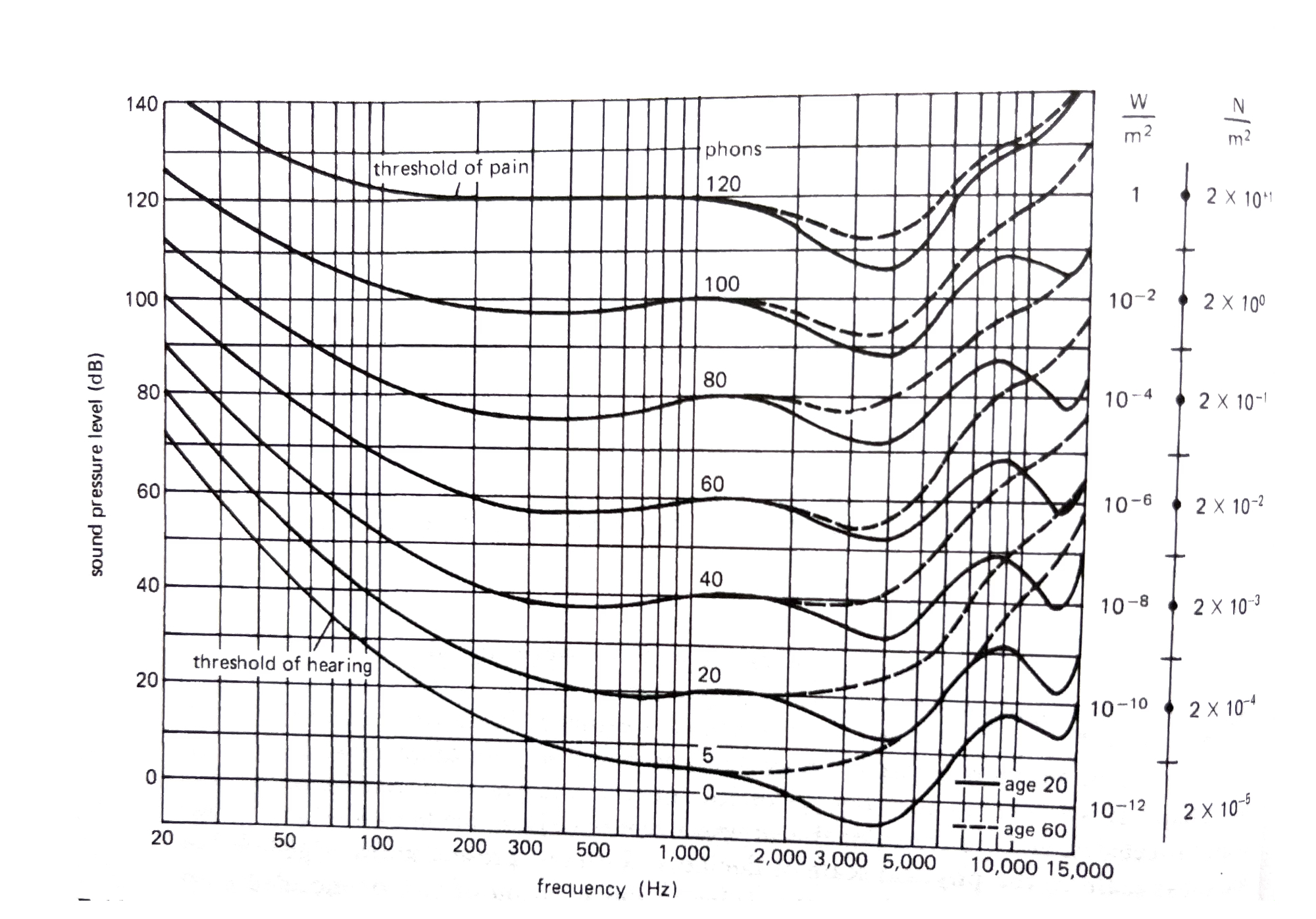
在3000到5000这个区间,人耳的灵敏度明显更高,要达到听起来同样响,只需要更低的声音强度。在低频和高频区,灵敏度都比较低。另外,随着年龄增长,中高频的灵敏度也明显下降,尤其是本身强度就比较低的声音。
持续时间与响度
一个简短的声音似乎更安静,因为它并没有激励人耳足够长的时间,即使它的峰值强度很大。当持续时间小于200ms时,响度感觉会随时间减少而减弱。
听觉疲劳——当纯音产生稳定声音并持续了一段时间后,它听起来似乎变安静了,一分钟以后,它的音量听起来似乎降低了一半。如果被打断,即便是很短暂的暂停,也能恢复初始响度。
[========]
叠加声源的响度
两个完全一样的声音同时响起,比如两把一样的小提琴同时演奏完全频率和振幅弯曲一致的音,这时的音量是否增加了一倍?
如果两个纯音分别都是60 dB,两个音叠加在一起,如果说音量变成了120 dB,这显然是不可能的,这个音量将刺痛我们的耳朵。即便用日常经验也可以猜测出来,音量绝不会是加倍的。
根据分贝的数学意义,肯定不能直接进行加减。不过,两个声音叠加到一起,意味着两份能量,那么能量是必然加倍的,于是我们可以利用度量声音能量强度的绝对量值“声强”进行计算。
如果一个声音的声强为 $I_1$,另一个声音与它完全一致,那么两个声音叠加一起的声强为$2I_1$。
一个声音的声强级可以表示为:$ SIL_1=10\lg\frac{I_1}{I_0}$,两个声音用c作为角标,表示combined sound,它的声强级为 $ SIL_c=10\lg\frac{2I_1}{I_0}$。那么,两个声强级之差可以进行计算:
$$ SIL_c-SIL_1=10\lg\frac{2I_1}{I_0}-10\lg\frac{I_1}{I_0}=10\lg2=3.01 dB$$
所以,两个完全一样的声音叠加后,音量会增加3dB。
这里没有涉及到具体的绝对声强值,因为两个声音完全一致,按照比例关系即可计算,比较方便。如果将具体的声强值代入计算,结果也是一样的。
example
10把完全一样的小提琴,演奏同样的一个60dB的音,音量会变成多少呢?
$$ SIL_c-SIL_1=10\lg10=10dB $$
所以叠加后为70dB。
如果两个频率一致、但音量不同的声音叠加到一起,同样可以用声强的绝对量度来计算,当然这次就不能把具体数值省略掉了。
example
两把一样的小提琴演奏同样的一个音,其中一把音量为60dB,另一把音量为65dB,最终的音量是多少?
60dB 对应 $1\times10^{-6} W/m^2$ 的声强(可以用声强级公式反推出来,但也可以查找相关的对应表),65dB 对应 $3\times10^{-6} W/m^2$ 的声强。因此,它们叠加后的声强为 $4\times10^{-6} W/m^2$,是较弱声音的4倍。现在代入前面的计算公式中:$ SIL_c-SIL_1=10\lg4=6dB $,叠加后的声音,相比较弱的那个单一声音增加6dB,所以最终是66dB。
[========]
对频率的感知
声音的频率对于人的感知来说就是音高。比如管弦乐队的标准音A的频率是440 Hz,对于人耳来说,它是一个音高为A的乐音。
前面已经提到人的频响范围在20 Hz~20 kHz,20岁以后这个上限就会降到16 kHz左右,之后随着年龄增长会继续下降。
对这个频率范围的一种分段描述如下:
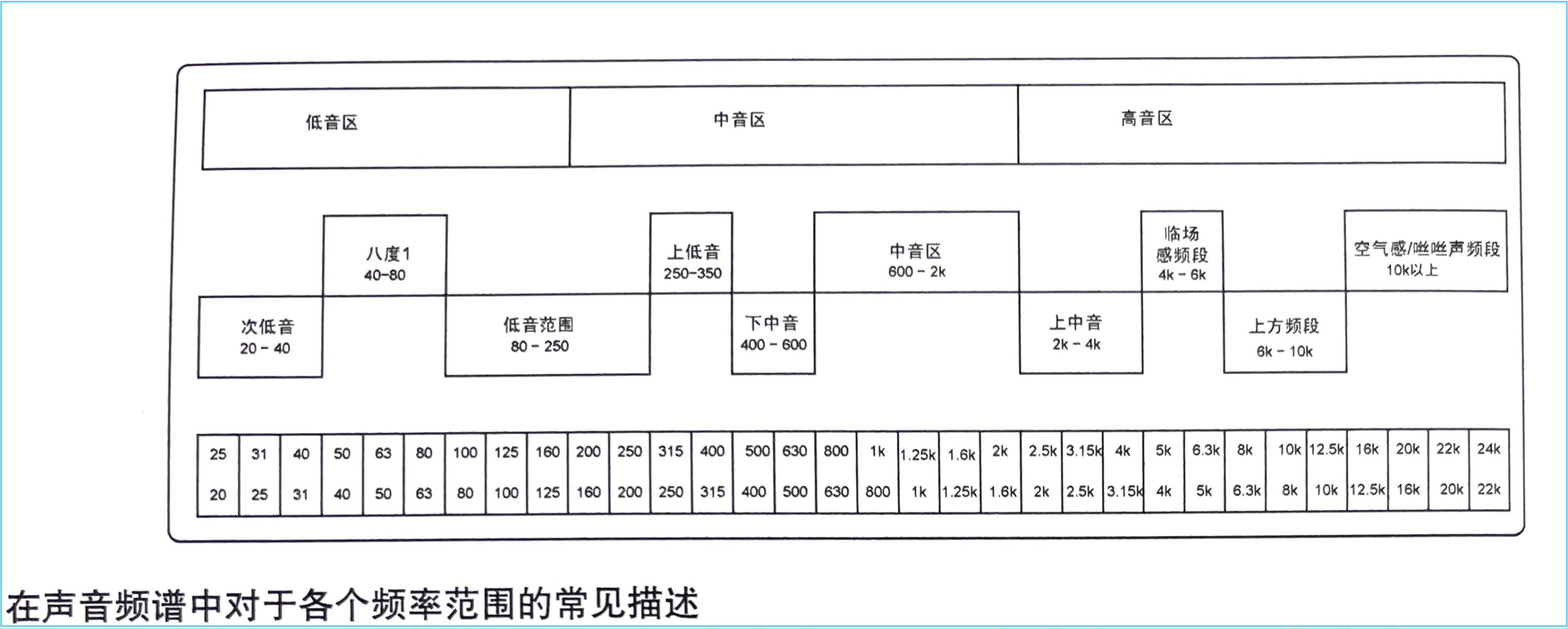
频率分辨 frequency discrimination
人对不同频率的感知是有极限的。分辨能力指的就是能够听出同时发声的两个不同频率(但非常接近)的纯音是两个单独的声音。如果它们的频率过于接近我们就听不出来是两个不同的音,它们会融合到一块变成一个音符。
所有复杂音都能够用不同频率、振幅、相位的纯音组合而成,而我们听觉系统中的耳蜗具有将一个复杂音解析出构成它的原始纯音的能力。但是这种分辨能力有限,如果要分辨两个不一样的频率,它们的差值需要超过一定的界限。
拍频/拍音现象 beats
两个频率非常接近的声音同时响起,近到无法分辨,这时我们会听到一种反复出现的类似颤音的效果,称为“拍频”或者“拍音“。在很多乐器中都有用到这个效果。
将两个有轻微相位差的波形叠加到一起,可以清楚看到这种效果的原理。
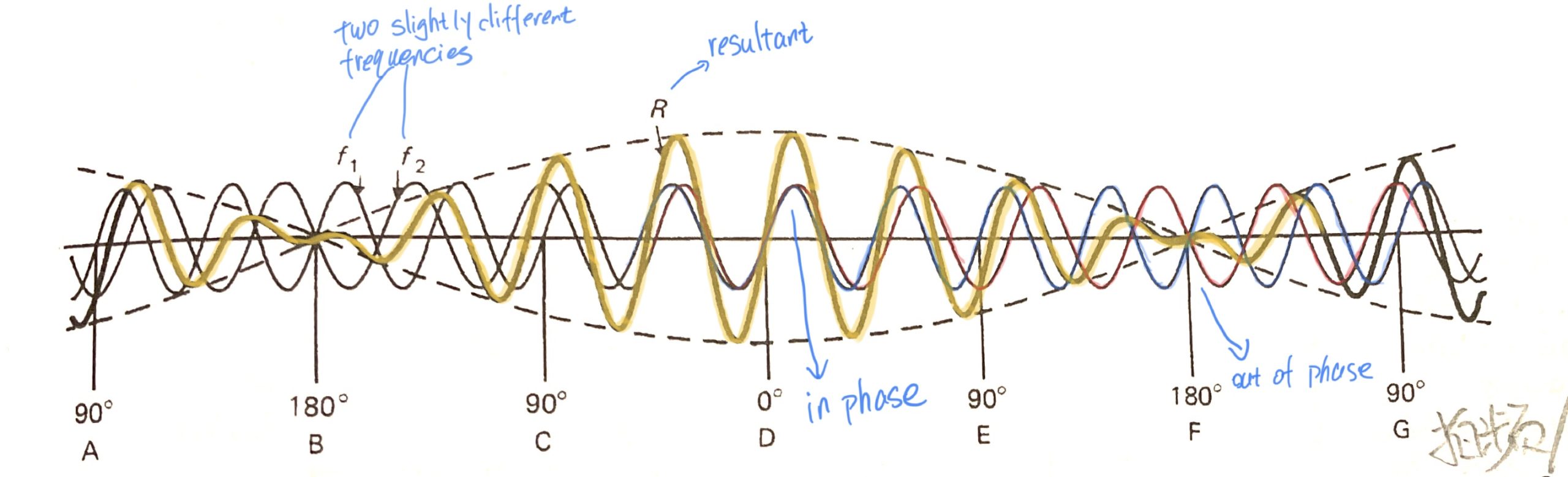
由于频率非常接近,两个波形加到一起后会周期性的“同相-异相-同相-异相...“,在他们异相(刚好反相)的时候,波形刚好被抵消,振幅降到零,但在同相时,振幅被加和。
从听觉系统的原理来说,两个接近的频率由于处于基底膜一个临界频带之内,无法分辨出两个频率。当差距变大到覆盖两个临界频带后,基底膜才能做出相应的反应,识别出不同的频率。
拍音现象 beats 被定义为由两个略有不同频率的声波振幅周期性重合所引起的声强脉动。
这个周期性的“拍音”的频率称为“差频”或“差拍” beat frequency,可以记作 $f_{bf}$ ,这个频率(不是音高频率,是周期性pulsation的频次,the resultant vibration pattern of varying amplitude),正是两个声音的频率之差,$f_{bf}=f_2-f_1$ ,设定 $f_2$ 代表略高一点的那个频率。
那么,人感知到的那个融合声音的音高是多少呢?
$f_{av}=\frac{f_1+f_2}{2} $ ,最终那个声音的频率是两个声音的平均值。
这种现象发生在频率差小于15Hz、响度也差不多的两个声音同时发声的情况中。最终听到的声音,其频率为二者的平均值,响度则是周期性变化的颤音效果。
临界频带
尝试一个实验,我们用软件生成两个完全一样的音,然后逐渐升高其中一个的音高,会体验到拍频。
当音高继续上调到10到15Hz左右时,拍频现象会消失,取而代之的是一种“粗糙感”。
当频率差终于勉强超过频率分辨的某个阈值后,我们开始听到两个音高不同的声音,这个时候,基底膜的两个共振区域勉强被激活了,不过“粗糙感”仍在。
继续升高,当频率差增大到一个被称为“临界频带”(记作 $\Delta f_{CB}$)的阈值后,粗糙感逐渐减弱,声音逐渐平滑,两个不同的声音越来越清晰。
以上分段的过程在下图中展示出来(分界线并不是明确的,每个人的感知能力不同。并且,高频、低频的分界区域也会有很大不同):
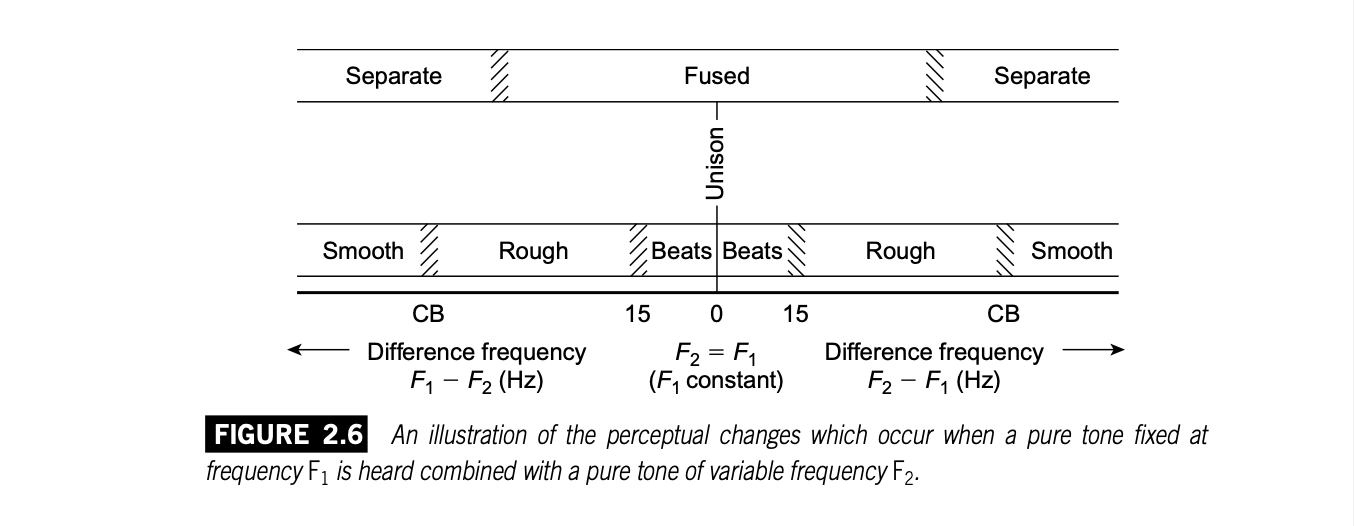

实验发现,临界频带几乎不受响度的影响,它与基底膜的结构有关。
这种现象只发生在两个耳朵同时听一个声源的情况。如果两个耳朵各听一个声音,以上现象均不存在。这也证实了它的确与听觉系统中基底膜的反馈有关。两个耳朵各自的耳蜗分别解析各自的声音,便不存在“两个频率落在同一个临界频带内”的情况。
临界频带模型源于把耳蜗看成一个在各频带之间具有有限分辨率的频谱分析仪。耳蜗有成千上万的细小绒毛。耳蜗的各个区域都被调谐到对应不同的频率,在各区域中每个绒毛都对应着一个小范围的频率。我们称其为“定位信息”,因为它与“刺激沿着基底膜在何处发生”有关,不应该把它与对声音的方向定位相混淆(对声音的方向定位指的是在人头之外的一个声源的位置)。
耳蜗是有有限数量的毛细胞组成的,所以对频率的分辨率是有极限的。在毛细胞与我们能够听到的可能频率之间并不存在一一对应的关系——如果一一对应的话大概只能听到约18000个离散频率。取而代之的是,我们把两类信息结合在一起:定时(一个波形的每个周期中神经元在何时产生神经冲动)和定位(临界频带中的一组神经元在何处谐振,这由它们处在基膜的哪个位置决定)。
一个独立的神经元仅能以某一速率产生神经冲动(据说最高到1kHz),但多个神经元的输出可以随后被组合起来,得到一个更好的分辨率。无论如何,这个过程不是线性的。
对临界频带带宽的不同定义:
带宽的具体数值在不同研究中可能有所差异,但一般来说,临界频带的带宽大约在100 Hz到2000 Hz之间。
- 梅尔刻度下,耳蜗的临界频带数量大约在20到30之间,并且每个临界频带的带宽通常为1倍频程或更大。
- 根据"Terhardt's ERB"(Equivalent Rectangular Bandwidth)模型,耳蜗内部的临界频带可以用一系列等效矩形带通滤波器来近似表示,每个滤波器具有1/3倍频程的带宽。
遮蔽效应 masking
在时间上相邻或频谱上相邻的不相关声音可以相互干扰。有时候,其中一个声音会完全淹没另一个,以至于那个声音不再被听到。
同时遮蔽 simultaneous masking
同时遮蔽是指一个声音恰好盖在另一个声音的上面。显然,通过叠加,两个声音混合成了一个,是我们对于单个声音的感知受到了影响。
在架子鼓中,军鼓、踩镲和底鼓占据了完全不同的频带,所以那些在同一拍上出现多个声音的节奏中,每件乐器的声音都是清晰可听的。如果两个声音相对近似,并且其中一个显著的更响一些,则较弱的那个声音将不会被听到。也就是说,我们无法区分这是两个声音的混合,还是我们听到的那个(产生遮蔽效果的)声音在单独发声。
基于临界频带遮蔽 critical band masking 的解释:每个临界频带一次只能从一个声音中转换信息。如果两个声音所包含的各频率分量(泛音)共享了同一个临界频带,那么这两个声音就融合在一起了。
-
带内遮蔽 in-band masking
如果一个声音所包含的内容完全处于另外一个声音的各临界频带所构成的某个子集中(频率范围完全被覆盖),那么后者将处于支配地位,并且会完全包含第一个声音。 这是MP3算法中使用的心理声学数据压缩的一个重要组成部分。 -
带间遮蔽 interband masking
在一个临界频带中的声音也可以被相邻的临界频带中的声音所遮蔽。如果一个窄带声音旁边有另外一个声音,该声音与上下两个相邻频带都相关,则这个窄带声音将被遮蔽。我们称另外那个声音发生了扩散,其扩散函数 spreading function 取决于频率和幅度。高频更容易被扩散遮蔽,因为频谱上频率较高的频带占据更宽的频率范围。
时域相邻遮蔽 temporal masking
被简短的时间间隔分隔开的声音会彼此影响。两个在时间上快速相继发生的声音会发生前向遮蔽forward masking 和后向遮蔽 backward masking 。
前向遮蔽中,一个较响的声音(masker)后面跟着一个较安静的声音(target),遮蔽声会暂时降低目标声的可听性或可察觉性,使其更难以感知,即使这个较安静声音有其自身的空间。这种遮蔽发生在100~200ms之后。
后向遮蔽中,较响的声音(masker)位于较安静声音的后面(target),在一小段时间里,遮蔽声会干扰目标声的感知,这种情况只能发生在30~100ms之前。
时域遮蔽是由听觉系统的生理和心理声学特性所造成的。它在音频编码、降噪算法、音频压缩技术以及了解不同声音的听阈和感知阈方面起着重要作用。
被遮蔽音的阈值增加
假设有一个音量较低勉强能被听到的800 Hz纯音,现在出现一个正常强度的400 Hz纯音,它使那个800音听不到了。把这个400 Hz的音称为masking tone,800那个称为masked tone。现在逐渐增加800的音量直到能勉强听到。这个过程所增加的音量就是所谓的 threshold increase of the masked tone,以分贝为单位。
贝尔实验室曾做了大量遮蔽效应方面的研究实验,被遮蔽音的阈值增加与那个较响声音的频率和声强有关。测量结果以图表的形式总结发表出来,以下是其中一部分有一定代表性的曲线图。
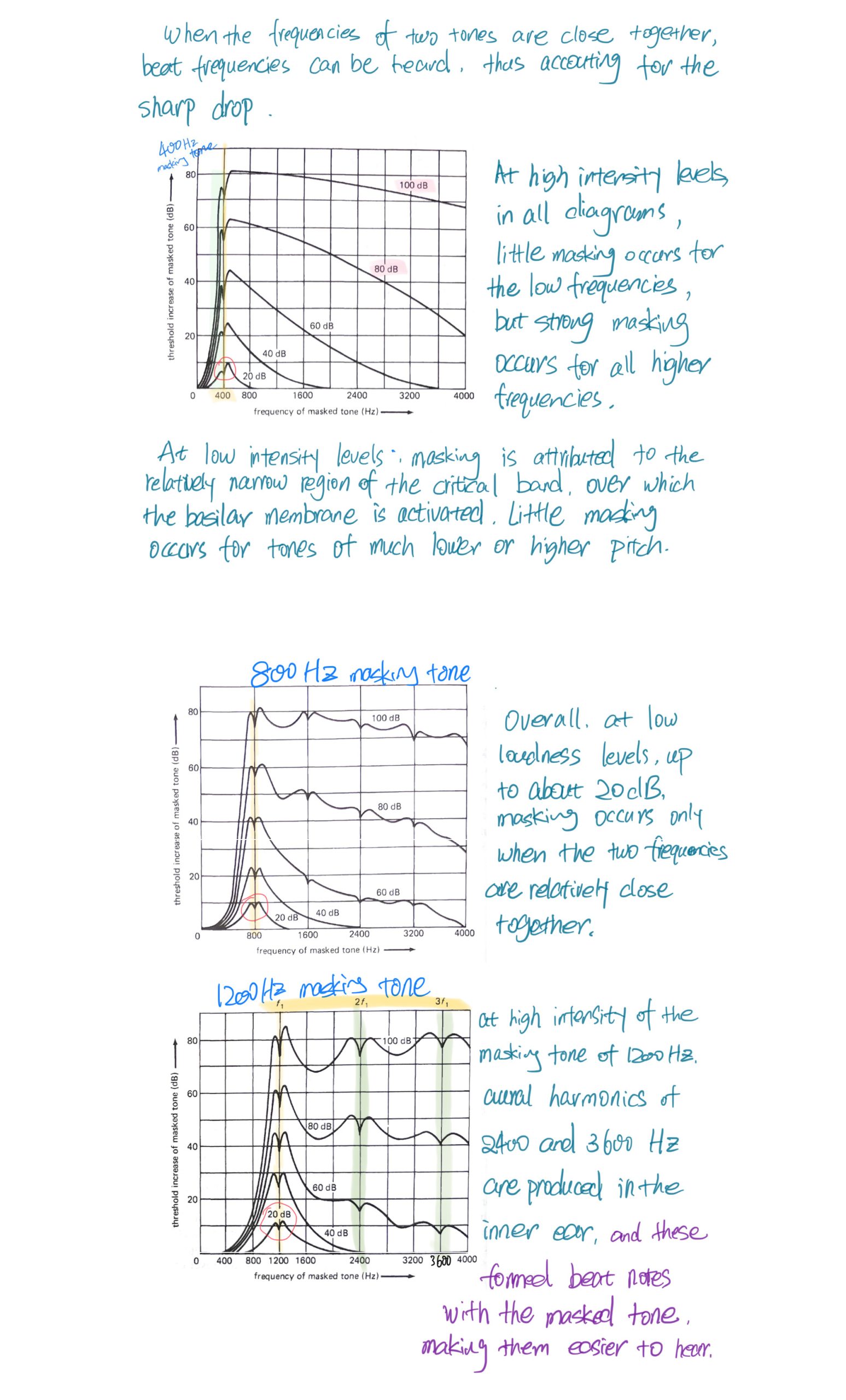
Part III 乐音、音色与频谱
构成一个声音的最基本要素——频率和振幅,决定了一个纯音的“根本身份”,但自然世界里的声音显然没有这么简单。面对复杂音时,一个更加抽象的声音要素必须考虑进来,那就是声音的波形 waveform,或者更复杂一点的说法——频谱 spectrum。
频率、振幅、频谱,这些都是声音的可测量的物理属性,对应人的主观感知的概念分别是音高、响度、音色 timbre。
基频与谐波
Partials
由简谐运动形成的波是正弦波,正弦波仅有一个单一的明确的频率。我们听到乐器发出的单个音符却是由许许多多不同频率的正弦波构成的。所有这些“组成成分”统称为partials(在不同语境下,partial可翻译为频率分量、分音、谐波等)。
将这些成分组合到一起形成一个复杂波的过程,就是所谓的“合成” synthesis;逆向过程——把一个复杂波中的组成成分拆解出来的过程就是“解析”analysis;
作为声波的正弦波,它所形成的“音”,叫做“纯音” pure tone。然而自然声音中不大可能会有纯音,由乐器发出的清晰明确的音符同样也是复杂音——由很多不同频率的纯音组合而成,这些构成成分就称为partials。其中最低的那个频率称为“基频” the fundamental,其他所有比基频高的partials就是“泛音” upper partials / overtones (这里泛音的概念比较笼统,此处所表达的含义也并非“谐波”,而是基频以外的所有频率分量的统称。实际的乐音当中,除了基频和谐波,也包含其他一些非整数倍频的分量,因此不能简单断言,一个有明确音高的乐音除了基频就是谐波)。
【基频or基音,谐频or谐波,只是基于不同语境(面向纯物理或面向音乐)的习惯说法,不再刻意区分】
在所有这些频率分量当中,有一些比较特殊,它们刚好是基频的整数倍,这些被称之为 “谐波” harmonics 。谐波以其相对基频的整数倍的“倍数”作为名称。比如一倍基频,那就是基频本身,称为“1次谐波” First harmonic,两倍基频的谐波就叫“2次谐波” Second harmonic...
【音乐家们习惯说的泛音,指的就是除基频以外的其他谐波。比如2次谐波就是第一次泛音。泛音似乎是早期说法,只是很多人仍然习惯用它。二者应避免同时混用。我只用“谐波”这一个说法。】
[========]
Timbre
我们听到一个声音会辨识出它的音高,这个音高是从声波的基频来辨别的。但是同样的音高,不同的乐器发出的声音“质感”——音色是不同的,正是因为它们各自的频率分量都很不一样,有自己的pattern。而且这些分量当中,并不全是谐波。那些与基频的关系不是刚好整数倍的那部分频谱,就称为“非谐波分量” inharmonic partial。打击乐器呈现出的声音中就有大量这样的“非谐和成分”。
当然,大部分乐音都是有谐波构成的,音乐的音阶体系也是基于谐波。
人感知到不同的频谱带来不同的声音“特质”,这个主观体验就是所谓的音色 timbre。频谱并不是一维的标量,而是一个数值矩阵。音色指的是一个静态的频谱,它带有基频和一系列谐波(泛音)。这是频域中的一张“快照”,并没有捕捉声音的演变过程。当我们谈论音色时,说的是一个由稳定频谱产生的瞬时的听觉感受。
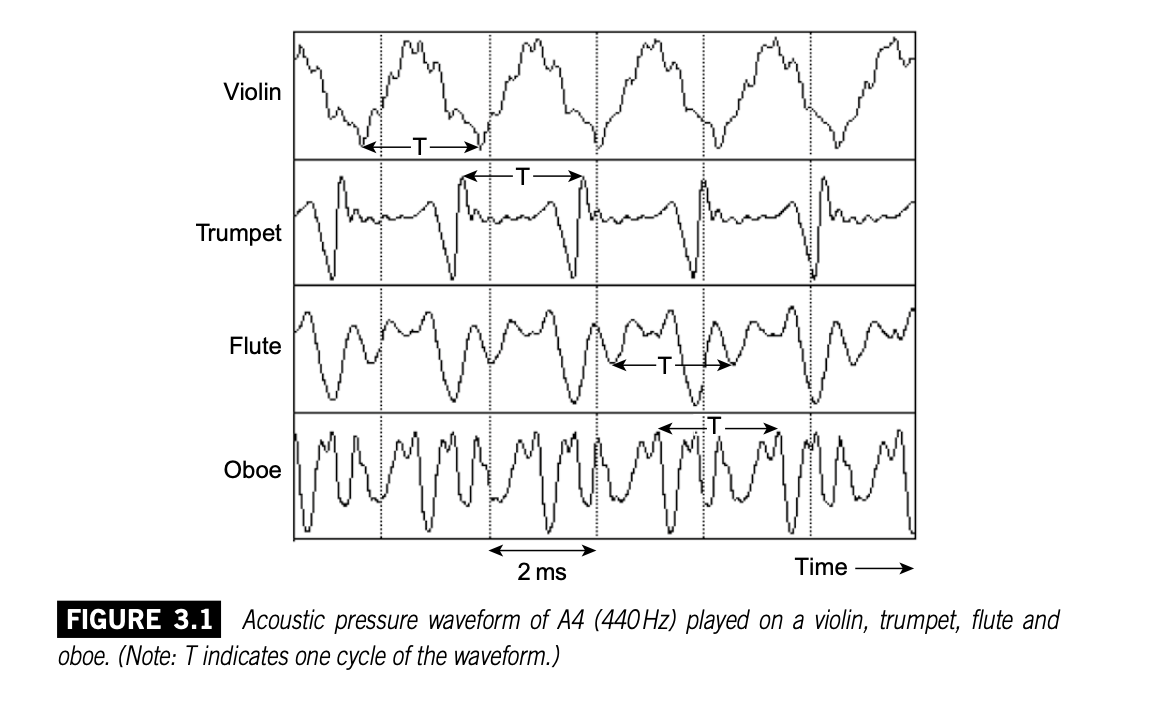
不同的乐器演奏同一个音符呈现出不一样的波形。虽然它们的周期和基频一致,但是各自的波形有许多不同的细节。人耳就是通过这些细节来辨识不同的音色。
乐器振动产生的声压作用于听者的鼓膜,从而决定了听觉基底膜上振动形态的建立,听觉系统根据这个振动形态对声源的频率成分进行分析。每种乐器在它的频谱上有一系列频率分量,听觉根据其频谱辨识不同的乐器。这一系列分量的振幅各有不同,上图四种乐器每个波形的振幅频谱如下:
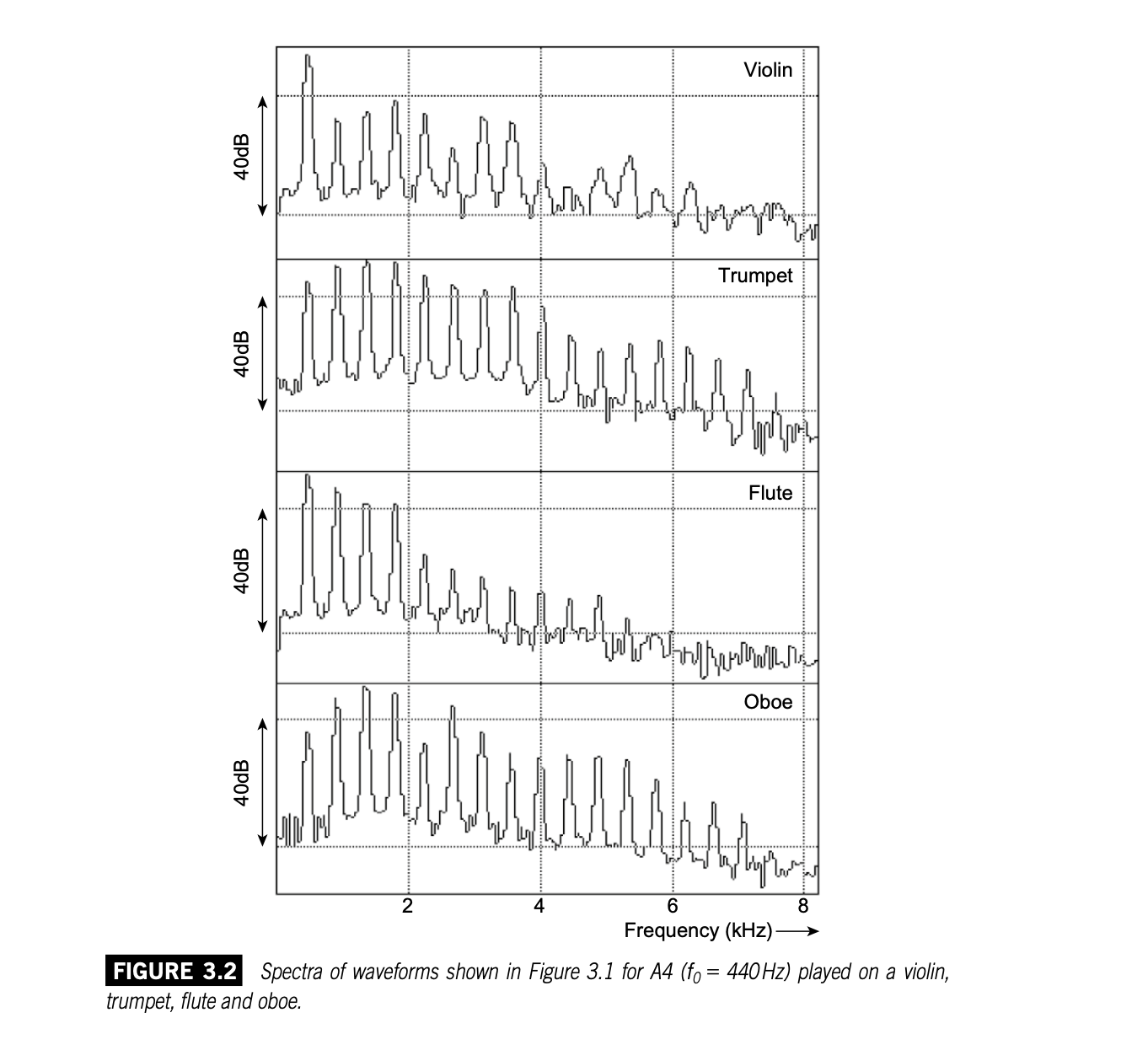
(那些清晰可见的波峰对应着前几次谐波的振幅)
[========]
Wave generation
现在已经知道,一个能被感知音高的声音都是由一系列谐波构成的,每个谐波是一个正弦波,由此就可以对声波进行分析与合成。
把一个声音中的各种成分拆解出来的设备称为analyzer,反过来将这些成分组合回去形成一个复杂音的设备就是synthesizer。
19世纪初提出的傅里叶理论告诉我们,每个周期性复杂波都可以拆解为一系列频率关系谐和的正弦波。这意味着随便哪个周期性声波都能用一系列纯音构成。
锯齿波
基本波形中的锯齿波的生成,是由基频加上所有整数倍的谐波,每个谐波的振幅为 $a, \frac{1}{2}a, \frac{1}{3}a, \frac{1}{4}a...$。如果相位不做调整,全部为零的话会生成这样的波形(共10次谐波):
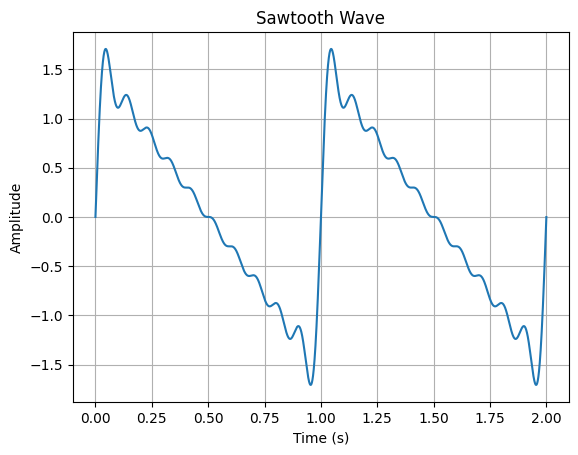
还可以做出方向相反的锯齿:
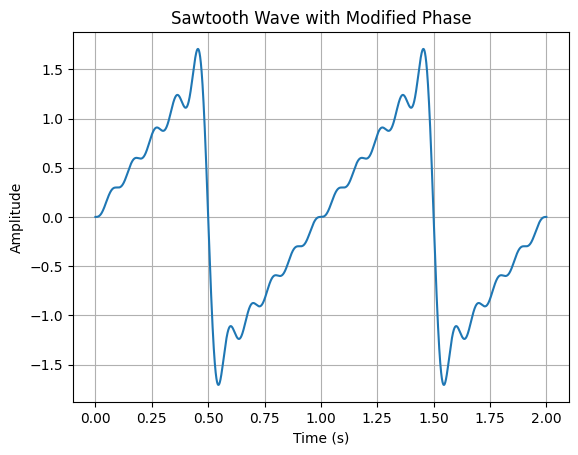
这是因为偶数次谐波的相位为180度,即振幅为负,与其他谐波反相。代码示例:
import numpy as np
import matplotlib.pyplot as plt
# 锯齿波参数
amplitude = 1.0 # 振幅
base_frequency = 1.0 # 基频率
num_harmonics = 10 # 谐波数量
# 时间范围和采样点数
duration = 2.0 # 波形持续时间(秒)
sampling_rate = 44100 # 采样率(每秒采样点数)
num_samples = int(duration * sampling_rate) # 总采样点数
# 时间轴
t = np.linspace(0, duration, num_samples, endpoint=False)
# 构建锯齿波形
sawtooth_wave = np.zeros_like(t)
for n in range(1, num_harmonics + 1):
frequency = n * base_frequency
phase = np.pi if n % 2 == 0 else 0.0 # 条件判断,偶数次谐波相位设为π,奇数次谐波相位设为0
harmonic_wave = amplitude / n * np.sin(2 * np.pi * frequency * t + phase)
sawtooth_wave += harmonic_wave
# 绘制锯齿波形
plt.plot(t, sawtooth_wave)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Sawtooth Wave with Modified Phase')
plt.grid(True)
plt.show()方波
构成方波的是所有奇数次谐波,其振幅则是$a, \frac{1}{3}a, \frac{1}{5}a, \frac{1}{7}a...$,相当于是把锯齿波中的偶数次谐波直接去掉了。
三角波
构成三角波的同样也是奇数次谐波,但是振幅下降极快:$a, \frac{1}{3^2}a, \frac{1}{5^2}a, \frac{1}{7^2}a...$,
振幅和相位同样有两种设计方式。一是全部保持同样的相位,另一种是类似前面锯齿波,0度和180度交替,也就是振幅正负交替。后一种方式会使得三角形以更快的速度变得尖锐。
第一种简单方式的代码及其生成图:
# 三角波参数
amplitude = 1.0 # 基准振幅
num_harmonics = 10 # 谐波数量
# 时间范围和采样点数
duration = 2.0 # 波形持续时间(秒)
sampling_rate = 44100 # 采样率(每秒采样点数)
num_samples = int(duration * sampling_rate) # 总采样点数
# 时间轴
t = np.linspace(0, duration, num_samples, endpoint=False)
# 构建三角波形
triangle_wave = np.zeros_like(t)
for n in range(1, num_harmonics + 1, 2): # 只包含奇数次谐波
frequency = n
harmonic_amplitude = amplitude / (n ** 2) # 按照给定规律计算谐波的振幅
phase = 0.0 # 相位设为零
harmonic_wave = harmonic_amplitude * np.sin(2 * np.pi * frequency * t + phase)
triangle_wave += harmonic_wave
# 绘制三角波形
plt.plot(t, triangle_wave)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Triangle Wave')
plt.grid(True)
plt.show()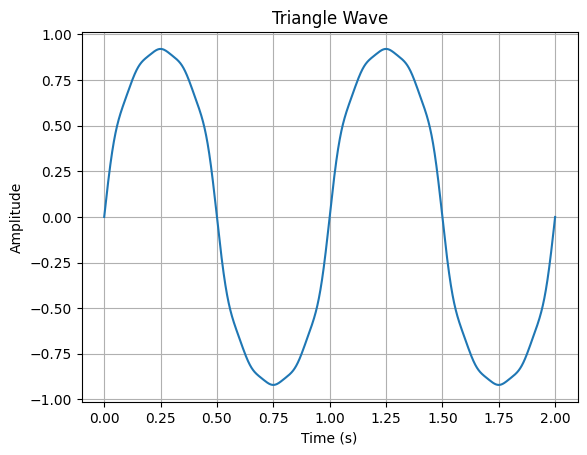
第二种方式的代码及其生成图:
import numpy as np
import matplotlib.pyplot as plt
# 三角波参数
amplitude = 1.0 # 基准振幅
num_harmonics = 10 # 谐波数量(只包含奇数次谐波)
fundamental_frequency = 1.0 # 基频(Hz)
# 时间范围和采样点数
duration = 2.0 # 波形持续时间(秒)
sampling_rate = 44100 # 采样率(每秒采样点数)
num_samples = int(duration * sampling_rate) # 总采样点数
# 时间轴
t = np.linspace(0, duration, num_samples, endpoint=False)
# 构建三角波形
triangle_wave = np.zeros_like(t)
for n in range(1, num_harmonics + 1, 2):
harmonic_amplitude = amplitude / (n ** 2) if (n // 2) % 2 == 0 else -amplitude / (n ** 2)
frequency = fundamental_frequency * n
harmonic_wave = harmonic_amplitude * np.sin(2 * np.pi * frequency * t)
triangle_wave += harmonic_wave
# 绘制三角波形
plt.plot(t, triangle_wave)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Triangle Wave')
plt.grid(True)
plt.show()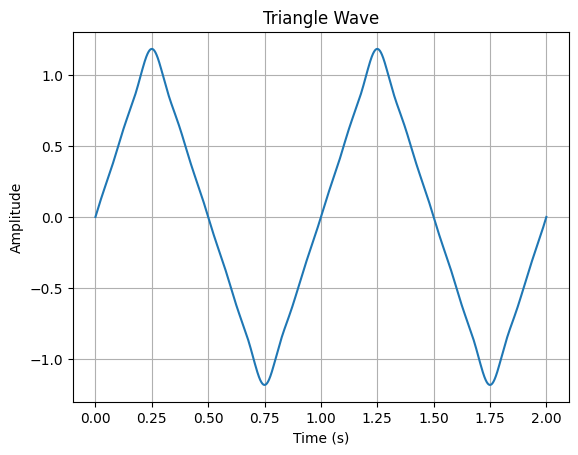
振幅正负交替的谐波在合成过程中会引入更多的奇次谐波,并且它们之间存在相位差。这种谐波的组合会导致波形在每个周期内快速变化,并且在交替点处出现陡峭的转折。当这些奇次谐波振幅正负交替时,它们对波形的形状会产生复杂的影响。例如,在交替点附近,正和负振幅的谐波会相互抵消,导致波形陡峭地转向。这种相互作用使得波形更加尖锐并且具有明显的三角形状。
[========]
Spectrum
谐波的相对振幅对最终声音的音色影响很大,呈现音色与质感的图表就是声音的频谱图,它表达的是各个频率的强度(或者说在整个声音中的“分量”),同时也可以一目了然的看出来整个频率的分布。
对于不同乐器具有独特音色的经验会给人一种“假想”:每种乐器应该有它自己的固定的一种波形特色(pattern),实际情况却复杂的多。有些乐器,比如法国号,不同频率区域和不同的声音强度下,音色听起来都会不一样,频谱远不止一种。所以同一个乐器的频谱也是变化多样的。
影响音色感知还有一个重要因素就是声音刚刚被建立起来的开头部分——起音 attack,同一根小提琴的弦,用弓擦弦和用手拨弦显然是截然不同的音色。
对于包络 envelope 的理解:构成一个声音的各个样点和波形形成了一种连续的“流”,根据这个系统中能量的变化,将其划分到有意义的结构框架中,是一种非常好用的分析与设计的方法。包络的四个阶段ADSR,可以应用于任何变化的性质上,比如幅度、频率、音色。合成中使用的各种控制包络常备缩写为ADSR,以反映这些变化阶段。
建立乐音的音色与频谱之间的关联还有一个更为重要的概念——共振峰 formant。某个乐音的共振峰指的是其声音频谱中能量高度集中的某个频段。
有共振/谐振的音色都带有一个尖锐狭窄的频谱,大多数频率都集中在一个或多个固定的频点周围。作为另外一种情形,当频谱是平坦均匀的分布时,我们称这个音色是平直或宽广的。类噪声源(镲片)能给出一个宽广平坦的音色,而木笛则给出一个尖锐共振的音色。很多声学乐器都有多个固定的共振。一个单一音符不能展现出这些共振,因为它不能告诉我们哪些来自于激励器(琴弦),哪些来自于共振体(琴身)但如果有两个或者更多不同的音符被演奏,那么共有的共振就变得明显了。在感知方面,我们把这种固定的共振特征称为一个共振峰formant。
300~1000赫兹内尖锐的共振和共振峰组合起来的声音听起来像人声。
在声音频谱研究中的一个惊人发现是,作为音高决定者的基频,却往往不是频谱中最响的那个,经常地,它还是相对较弱的一个成分。那些基频以上的、幅度较强的频率分量也许决定了一个乐器的音色。
Spectral centroid
对音色的描述中,会用到一个主观标度:明亮度。明亮的声音比暗淡的声音具有更多的高频谐波。但是具有一些较响的高频并不足以让一个声音明亮。对一个声音是明亮还是灰暗的最好度量是找到它的频谱的“重心”或频谱质心 spectral centroid。这是一个加权的方式,通过把每个临界频带中各个频率的强度(幅度or能量)加在一起并除以所有频带的总和就得到了质心。对于N个临界频带,假设每个频带的中心频率为 $f_n$,包含能量为 $x_n$。
$$fc=\frac{\sum\limits{n=0}^{N-1} f_n xn}{\sum\limits{n=0}^{N-1}x_n} $$
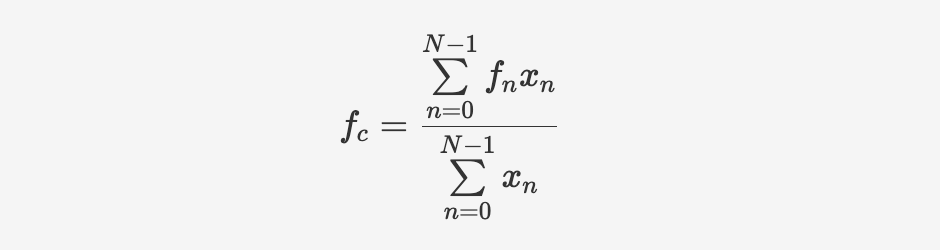
频谱质心代表了信号在频域上的中心位置或平均频率。它是通过对每个频率分量的频率与相应幅度(或能量)之积进行加权平均得到的。频谱质心可以指示声音在频率上的核心位置或主要成分所在的频率。它表示声音信号在频域上的集中程度,即哪个频率分量对整个声音起到最大的贡献。较低的频谱质心意味着声音更集中在低频区域,而较高的频谱质心则表示声音更集中在高频区域。
因此,频谱质心可以用来描述声音在不同频率上的能量分布情况,并提供有关声音特征和调性的信息。
频谱还必须要有足够的连续性才能产生明亮的音色。一个主要为低频且只有一个孤立的高频分量的频谱将被听成是一个灰暗的声音加上一个单独的“人造声”在上面。在很多音色空间研究(Wessel 1973; Grey 1975, Moorer, Grey 和Snell 1977-1978)中,明亮度作为一种标度维度被用来描绘摩擦和非线性过程的特征(被拉奏的琴弦和号角)。声音的起音 Attack 部分对明亮度的感知非常重要。如果声音以一个明亮的瞬态信号开始,那么这个声音的其余部分也会向明亮的方向偏重。一个灰暗的音色具有较低的频谱质心,或是在语音范围内不能有确定的谐波结构,这类声音听起来是阻尼的、含混不清的。
